Pi

From Conservapedia
This is an old revision of this page, as edited by RolandPlankton (Talk | contribs) at 22:27, March 20, 2012. It may differ significantly from current revision.

Jump to: navigation, search

Pi or or π is the name or symbol for an important mathematical constant, which appears in many branches of mathematics. π was originally defined in geometric terms as the ratio of the circumference of a circle to its diameter. A simple well-known formula using π gives the area of a circle as: π * radius * radius. [1]

An approximate value for π is 3.141592653... The exact value can never be expressed as a fraction or as a decimal number, regardless of how many digits are used (Lambert[2] proved this in 1761 by showing that π is an irrational number, which means that it can't be expressed as a fraction; Lindeman[3] went further in 1882 and proved that π is a transcendental number which means that it can't be expressed as the solution to any simple equation).

The approximate value quoted above is accurate enough to calculate the circumference of a circle of the size of the Earth with an error of only about 1 millimetre. For rough approximations, the fraction 22/7 (= 3.142857...), correct to 2 decimal places, is sometimes used. A more accurate fractional approximation is 355 / 113 (= 3.14159292...), which is correct to 6 decimal places.

History

The Greek letter π is the sixteenth letter of the Greek alphabet. It was first used with its current meaning in 1706 by a Welsh mathematician William Jones [4] because it is the first letter of the Greek word for perimeter (the circumference of a circle is its perimeter).

Mathematicians have worked for centuries to calculate to more and more decimal places. To some extent, the progress of mathematics—or at least of computation—can be gauged by the progress in the number of digits to which has been calculated.

Some ancients expressed by using fractional approximations. Papyrus of Ahmes, dated c. 1650 B.C., shows that ancient Egyptians had value 3 1/6 = 3.167). The Babylonian value from the same era was 3 1/8 = 3.125[5]. Both these values are accurate to within 1 percent. Note that the value 22/7 (3 1/7) is still used today.

Archimedes of Syracuse (287-212 BC) carried out "the first theoretical calculation" of .[6] He said it was between 223/71 and 22/7. This is ten times better than the Egyptian and Babylonian values: within 0.04% of .

In 1873, Abraham Shanks spent twenty years calculating to 707 places, but made a mistake in his calculation and only 527 of them were correct. When electronic computers were developed, was soon calculated to tens of thousands, millions, and billions of places. As of 2002, the record is held by Yasumasa Kanada of Tokyo University at 1,241,100,000,000 digits.[7] That result was never printed out.

Pi in mathematics

It's impossible to overestimate the importance of (and e) for mathematics. Both values are intrinsically tied, e.g. by Euler's identity

.

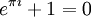Recreation

Memorizing is a challenge that appeals to some people. Mnemonics have been devised. Counting the letters in each word of the phrase "Now I want a drink—alcoholic, of course" gives to seven places (which is more than enough for all ordinary purposes). Numerous other mnemonics of this kind have been devised; in 1995, Michael Keith wrote one entitled Near a Raven which simultaneously parodies Edgar Allen Poe's poem The Raven, while encoding to 740 places.

March 14 marks Pi Day, a holiday on which the mathematical constant is celebrated. The date, 3/14, comes from the first three digits of ; some people begin their celebration at 1:59 pm, derived from the following three digits.

Approximation Day is a similar holiday, celebrated on 22nd July (from the approximation 22/7). [8]

is approximately:

3.14159265358979323846264338327950288419​7169399375​1058209749​4459230781​6406286208​9986280348​2534211706​7982148086​5132823066​4709384460​9550582231​7253594081​2848111745​0284102701​9385211055​5964462294​8954930381​9644288109​7566593344​6128475648​2337867831​6527120190​9145648566​92...

Greek Language Usage

This letter's name is pronounced the same as its equivalent Latin letter in English (P), and has the phonetic value, /p/.

Does the Bible attempt to define Pi?

Virtually all serious students of the Bible say no. Still, critics frequently claim that the Bible contains an incorrect value for , and the question is raised frequently enough to earn mention in the Skeptics Annotated Bible.

The claim is based on a verse in the first book of Kings:

He made the Sea of cast metal, circular in shape, measuring ten cubits from rim to rim and five cubits high. It took a line of thirty cubits to measure around it. 1_Kings 7:23 (NIV)

Thus, critics say, the Bible claims that the value of is 3, and is therefore in error. However, there are a number of assumptions in this claim, any of which might invalidate the argument if wrong:

  • That the tools and system of measurement available to the builders were sufficiently accurate to distinguish between 3 and pi.
  • That the phrase translated as "circular in shape" means perfectly circular, not simply "round" as an ellipse is round.
  • That the Bible is trying to provide a value for , and not merely describing the historical event of building this object.[9]
  • That a value is wrong simply because it is imprecise. To the nearest whole number, the value is correct[9], and it was quite common at the time to round to whole numbers.[10]
  • That both the diameter and the circumference are measuring the same edges. Since the sides of any practical vessel have thickness, it is possible that the diameter is an outside measurement and the circumference is an inside measurement.[10]
  • That both the diameter and the circumference are measuring the same part of the object. The object is also described as having an outward-turned rim. The easiest places to measure the diameter would be across the wider rim, and the easiest place to measure the circumference would be around the body below the rim.[11]

Common sense and a rudimentary knowledge of the Bible should cause one to question whether it sets out to define mathematical concepts. The creation of a "sea of cast metal" by human beings in ancient times, without modern construction tools and measuring equipment, does not require nor could it utilize a precise value for pi. An even more fundamental objection is that pi is an irrational number, and therefore has an infinite number of digits. (A "closed form" of pi does exist, but requires mathematical notation that was invented many centuries later.) A decimal expression of pi could not "fit" in the Bible, or in any other finite text.[9]

References

  1. ↑ The Circle Area Formula. Retrieved on 2012-02-13.
  2. ↑ Biography of Johann Heinrich Lambert. Retrieved on 2012-02-12.
  3. ↑ Biography of Carl Louis Ferdinand von Lindemann. Retrieved on 2012-02-12.
  4. ↑ A history or Pi. Retrieved on 2012-02-11.
  5. ↑ Boyer, A History of Mathematics, 2nd Edition
  6. ↑ Pi through the ages
  7. ↑ http://www.super-computing.org/pi_current.html
  8. ↑ USA Today (3/14/2007) - Pi-day
  9. ↑ 9.0 9.1 9.2 Discussion re rounding Pi. Retrieved on 2012-02-10.
  10. ↑ 10.0 10.1 Is the Bible wrong about pi?. Retrieved on 2012-02-10.
  11. ↑ Does the Bible say Pi equals 3.0?. Retrieved on 2012-02-10.

See Also

Retrieved from "https://conservapedia.com/index.php?title=Pi&oldid=969321"