Difference between revisions of "Definite integral"
From Conservapedia
(See Also) |
DavidB4-bot (Talk | contribs) (clean up & uniformity) |
||
| (14 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| + | {{Math-h}} | ||
| + | |||
A '''definite integral''' is an [[integral]] with upper and lower limits. | A '''definite integral''' is an [[integral]] with upper and lower limits. | ||
| + | |||
| + | [[Image:Definiteintegralnv7.gif|thumb|A definite integral.]] | ||
| + | |||
| + | ==Definite Integrals== | ||
| + | |||
| + | |||
| + | |||
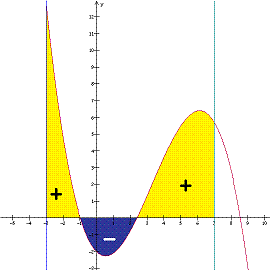
| + | A definite integral is the area under the curve between two points on the function. In the picture below, the yellow area is "positive" and the blue area is "negative". The integral is evaluated by adding the positive area together and subtracting the negative area. | ||
| + | |||
| + | [[Image:Definiteintegralnv7.gif]] | ||
If the function f(x) is real rather than complex, then the definite integral is also known as a Riemann integral. | If the function f(x) is real rather than complex, then the definite integral is also known as a Riemann integral. | ||
| − | |||
| − | |||
| − | [[ | + | == Solving Definite Integrals == |
| + | Solving a definite integral usually has two main steps: [[integration]] and [[subtraction]]. | ||
| + | |||
| + | Sometimes approximations, such as the Riemann Integral or [[Simpson's rule]] are used. These approximations are used when: | ||
| + | *The exact answer is not needed, only a close approximation. (Common in [[Engineering]]) | ||
| + | *The rule for integration is very complex. (Such as <math>\int e^{x^2}\,dx</math>) | ||
| + | *The rule for integration is simply unknown. (Such as <math>\int \zeta(x)\,dx</math>, the [[Zeta function]]) | ||
| + | |||
| + | == Example 1== | ||
| + | |||
| + | {| class="infobox" style="text-align:center;" | ||
| + | <table class="infobox" style="float: right; text-align: center; font-size: 100%; clear:right; background:white; border: 2px solid blue;" cellspacing="0" cellpadding="2" width="33%"> | ||
| + | |- | ||
| + | |[[Image:Firstexampledintegralsqa9.png|300px|Click on the image to get a better view.]] | ||
| + | |- | ||
| + | |A graph representation of <math>f(x)</math> in Example 1. | ||
| + | |- | ||
| + | |The ''thin blue line'' is f(x). | ||
| + | |- | ||
| + | |The ''yellow'' is what we add to get the value of the integral. It is the '''area'''. | ||
| + | |- | ||
| + | |The ''vertical green line'', the '''lower bound''', is at -3 because the lower bound of the definite integral is located at -3. | ||
| + | |- | ||
| + | |Likewise, the ''red line'' is the '''upper bound''', which is at 5. | ||
| + | |- | ||
| + | |Click on the image to get a better view. | ||
| + | |} | ||
| + | |||
| + | |||
| + | This is a very simple definite integral: | ||
| + | :<math>\int_{-3}^{5} x^2 dx</math> | ||
| + | |||
| + | === Integration === | ||
| + | |||
| + | <br />Using [[indefinite integral|indefinite integration]], it can be shown that: | ||
| + | :<math>\int x^2dx = {1 \over 3} x^3 = F(x)</math> | ||
| + | <br />Note that <math>F(x)</math> is the indefinite integral of <math>f(x)</math>. | ||
| + | |||
| + | === Subtraction === | ||
| + | |||
| + | <br />Now, plug <math>5</math> and <math>-3</math> into the new expression and subtract, as shown by the [[Fundamental Theorem of Calculus]]. | ||
| + | : <math>F(5) = {1 \over 3}5^3 = {125 \over 3}</math> | ||
| + | : <math>F(-3) = {1 \over 3}(-3)^3 = {-27 \over 3}</math> | ||
| + | <br />And subtract: | ||
| + | : <math>{125 \over 3} - {-27 \over 3} = {125 \over 3} + {27 \over 3} </math> | ||
| + | : <math>= {152 \over 3}</math> | ||
| + | |||
| + | == Example 2 == | ||
| + | This is a more complex definite integral that requires [[Partial fractions in integration|partial fractions]] to solve: | ||
| + | : <math>\int_4^{12}\frac{3x+11}{x^2-x-6}dx </math> | ||
| + | === Integration === | ||
| + | <br />See the [[Partial fractions in integration]] page for how to integrate the above expression (it is the example). | ||
| + | <br />As shown on the page mentioned above: | ||
| + | : <math>\int\frac{3x+11}{x^2-x-6}dx=4ln|x-3|-ln|x+2|+c</math> | ||
| + | |||
| + | === Subtraction === | ||
| + | |||
| + | This means that we can now subtract: | ||
| + | : <math>\left [ 4ln|12-3|-ln|12+2|+c \right ] - \left [ 4ln|4-3|-ln|4+2|+c \right ]</math> | ||
| + | : <math>= \left [ 4ln|9|-ln|14|+c \right ] - \left [ 4ln|1|-ln|6|+c \right ]</math> | ||
| + | : <math>= 4ln|9|-ln|14| - 4ln|1| + ln|6|</math> | ||
| + | : <math>= 4ln|9|-ln|14| + ln|6|</math> | ||
| + | : <math>\approx 7.94160...</math> | ||
| + | <br />Note the following: | ||
| + | * <math>ln(1) = 0</math> | ||
| + | * The <math>c</math> on each side cancels out because we have <math>c-c</math> | ||
| + | * <math>ln|6|</math> becomes positive because it was <math>-(-ln|6|)</math> | ||
| + | |||
| + | == See also == | ||
| + | |||
| + | *[[Integral]] | ||
| + | *[[Indefinite integral]] | ||
| + | |||
| + | |||
| + | [[Category:Calculus]] | ||
| + | |||
| + | [[Category:Integration]] | ||
Latest revision as of 11:32, July 13, 2016
|
This article/section deals with mathematical concepts appropriate for late high school or early college. |
A definite integral is an integral with upper and lower limits.
Contents
Definite Integrals
A definite integral is the area under the curve between two points on the function. In the picture below, the yellow area is "positive" and the blue area is "negative". The integral is evaluated by adding the positive area together and subtracting the negative area.
If the function f(x) is real rather than complex, then the definite integral is also known as a Riemann integral.
Solving Definite Integrals
Solving a definite integral usually has two main steps: integration and subtraction.
Sometimes approximations, such as the Riemann Integral or Simpson's rule are used. These approximations are used when:
- The exact answer is not needed, only a close approximation. (Common in Engineering)
- The rule for integration is very complex. (Such as
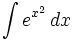) - The rule for integration is simply unknown. (Such as
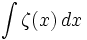, the Zeta function)
Example 1
|
A graph representation of  in Example 1.
|
| The thin blue line is f(x). |
| The yellow is what we add to get the value of the integral. It is the area. |
| The vertical green line, the lower bound, is at -3 because the lower bound of the definite integral is located at -3. |
| Likewise, the red line is the upper bound, which is at 5. |
| Click on the image to get a better view. |
This is a very simple definite integral:
Integration
Using indefinite integration, it can be shown that:
Note that 
is the indefinite integral of .
Subtraction
Now, plug 
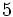and 
into the new expression and subtract, as shown by the Fundamental Theorem of Calculus.
And subtract:
Example 2
This is a more complex definite integral that requires partial fractions to solve:
Integration
See the Partial fractions in integration page for how to integrate the above expression (it is the example).
As shown on the page mentioned above:
Subtraction
This means that we can now subtract:
Note the following:
-
- The
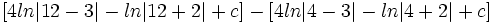
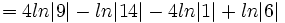
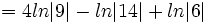
on each side cancels out because we have 
-
becomes positive because it was 
