Differentiation
Algebraic differentiation is an important part of calculus, an essential branch of mathematics in the modern age. This mathematical tool is denoted by the expression dy/dx, and has a pivotal role to play in a wide range of fields. For example, differentiation can be used in mechanics to find the acceleration of an object from a velocity-time graph.
Essentially, differentiation is employed as a means to calculate the gradient or rate of change at a particular value for a given function, f. Consequently, it can be used to calculate velocity from a displacement-time graph, or acceleration from a velocity-time graph. Furthermore, it can be used to calculate the rate of cooling from a temperature-time graph. These are a few examples of the applications of differentiation.
When defined from the first principals, the derivative of a function is the gradient of a function over  . If
. If 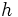 is allowed to appoach 0 then the gradient approches the gradient at the point
is allowed to appoach 0 then the gradient approches the gradient at the point  :
:
Alternative notation also commonly found is  and
and  .
.
In classical mathematics, a function can be be differentiated using the general formula:
(Proving this is a worth while exercise).
For example, if 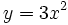 , the derivative with respect to
, the derivative with respect to  is
is
Thus the derivative is a measurement of how a function changes when the values of its inputs vary. Having calculated the derivative, the original input (in the above example, x) can be substituted in to work out the gradient. Moreover, differentiation can be employed to calculate the maxima and minima of a function (e.g. to ascertain the maximum velocity of an object in a function defining how its displacement varies with time), whereby dy/dx=0.
Differentiation Rules
The roots of differentiation are profoundly linked with tangency; ergo, this aspect of mathematics can first be perceived to have been developed during the time of the Ancient Greeks through the work of Greek geometers like Euclid, Sanath and Archimides.


