Difference between revisions of "Gauss's Law"
From Conservapedia
| Line 9: | Line 9: | ||
where <math>\Phi</math> is the electric potential (flux), <math>\vec{E}</math> is the [[electric field]], <math>\mathrm{d}\vec{A}</math> is a differential area on the closed surface ''S'' with an outward facing [[surface normal]] defining its direction, <math>Q_\mathrm{A}</math> is the charge enclosed by the surface, <math>\rho</math> is the charge density at a point in <math>V</math>, <math>\varepsilon_o</math> is a constant for the [[permittivity]] of free space and the integral <math>\oint_S</math> is over the surface ''S'' enclosing volume ''V''. | where <math>\Phi</math> is the electric potential (flux), <math>\vec{E}</math> is the [[electric field]], <math>\mathrm{d}\vec{A}</math> is a differential area on the closed surface ''S'' with an outward facing [[surface normal]] defining its direction, <math>Q_\mathrm{A}</math> is the charge enclosed by the surface, <math>\rho</math> is the charge density at a point in <math>V</math>, <math>\varepsilon_o</math> is a constant for the [[permittivity]] of free space and the integral <math>\oint_S</math> is over the surface ''S'' enclosing volume ''V''. | ||
[[category:physics]] | [[category:physics]] | ||
| + | [[Category:Electrical engineering]] | ||
Revision as of 05:11, July 26, 2007
Gauss's Law states that the electric flux through a closed surface is proporational to the electrical charge inside. This holds true regardless of the volume or shape of the closed surface. This is one of the most fundamental principles of electrodynamics, and is a Maxwell equation.
In integral form, Gauss's Law is this:
where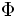 
is the electric potential (flux), 
is the electric field, 
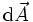is a differential area on the closed surface S with an outward facing surface normal defining its direction, 
is the charge enclosed by the surface, 
is the charge density at a point in 
, 
is a constant for the permittivity of free space and the integral 
is over the surface S enclosing volume V.
