Difference between revisions of "Kinetic Energy"
(username removed) (Small addition about rotational kinetic energy) |
(username removed) (Added derivation) |
||
| Line 63: | Line 63: | ||
== Kinetic Energy in Relativity == | == Kinetic Energy in Relativity == | ||
| − | + | In [[relativity]], kinetic energy can be expressed as: | |
| − | <math> | + | <math> K = (\gamma - 1) m_0 c^2 </math> |
| − | where <math>\gamma</math> is the Lorentz factor | + | where |
| + | :<math>\gamma</math> is the [[Lorentz factor]] | ||
| + | :<math>m_0</math> is the [[rest mass]] | ||
| + | :<math>c</math> is the [[speed of light]] | ||
| − | + | ===Derivation=== | |
| − | <math> K = (\gamma - 1) m_0 c^2 </math> | + | The kinetic energy is the [[work|work done]] accelerating a particle from rest to some speed <math>v</math>. Suppose the particle is at rest at <math>x_1</math> and speed <math>v</math> at position <math>x_2</math>. Hence: |
| + | |||
| + | <math>K = \int^{x_2}_{x_1} \vec{F} \dot d \vec{x}</math> | ||
| + | |||
| + | Since <math>\vec{F} = \vec{F}_{\perp} + \vec{F}_{\parallel}</math>, and a perpendicular force does no work, we can ignore the perpendicular component and write: | ||
| + | |||
| + | <math>K = \int^{x_2}_{x_1} F_{\parallel} dx = \int^{x_2}_{x_1} \gamma^3 m_0 a dx</math> | ||
| + | |||
| + | Since <math>a \, dx = \frac{dv_{\parallel}}{dt} dx = \frac{dx}{dt} dv</math>, we find the integral can be rewritten as: | ||
| + | |||
| + | <math>K = \int^{v_2}_{v_1} \frac{mv}{(1- \frac{v^2}{c^2})} dv</math> | ||
| + | |||
| + | where <math>v_1</math> is the initial speed and hence 0 by definition and <math>v_2</math> is the final speed. | ||
| + | |||
| + | Performing the integration reveals the kinetic energy as: | ||
| + | |||
| + | <math>K=(\gamma -1)m_0 c^2</math> | ||
==References== | ==References== | ||
Revision as of 16:16, September 23, 2016
Kinetic energy represents the energy associated with the motion of an object.[1] It is defined as the work done by a force to accelerate that object from rest to some speed 
, in the absence of any other forces acting upon the object. Kinetic energy is a scalar and has the same units as work (i.e. Joule).
Contents
Classical mechanics
Translational kinetic energy
In classical mechanics, the translational kinetic energy of a ridid object, 
, can be found as:
Where
is the Rotational kinetic energy
The rotational kinetic energy of a rigid object is:
Where
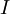is the moment of inertia of the object
is the angular velocity of the object
Work-Energy theorem
The change of kinetic energy is equal to the total work done on it by the resultant of all forces acting on it. For a point mass this can be expressed as:
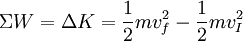
Where
is the initial 
is the final Note that if the mass of an object is increased, the increase in kinetic energy increases linearly; if the velocity of an object is increased, the increase in kinetic energy increases quadratically. For example, doubling the mass of an object doubles its kinetic energy; doubling its velocity quadruples its kinetic energy.
Derivation of translational kinetic energy
The work done by a force accelerating an object from rest, which is the kinetic energy is:
From Newton's second law, the force,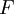 
, is 
. Hence we can make the substitution and use the chain rule
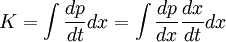
This is the same as
In classical mechanics, momentum is given by 
. Differentiating and substituting into the above equation results in
We want to integrate between 0 and the speed of the object, 
as this defines kinetic energy. Performing the integration reveals that the kinetic energy is, as expected, the following:
A similar method may be used to derive the formula for rotational kinetic energy.
Kinetic Energy in Relativity
In relativity, kinetic energy can be expressed as:
where
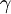is the Lorentz factor
is the rest mass
is the speed of light
Derivation
The kinetic energy is the work done accelerating a particle from rest to some speed . Suppose the particle is at rest at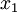 
and speed at position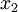 
. Hence:
Since 
, and a perpendicular force does no work, we can ignore the perpendicular component and write:
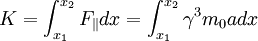
Since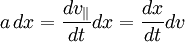 
, we find the integral can be rewritten as:
where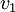 
is the initial speed and hence 0 by definition and 
is the final speed.
Performing the integration reveals the kinetic energy as:
References
- ↑ Serway and Beichner, Physics for Scientists and Engineers, Fifth Edition
