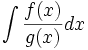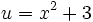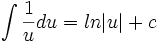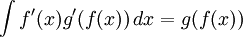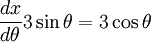Difference between revisions of "Methods of integration"

From Conservapedia
Jump to: navigation, search
m (added a missing period)
m (→‎Algebraic Substitution: Tidy up formatting)
(23 intermediate revisions by 7 users not shown)
Line 1: Line 1:
−
This article details several methods of [[integral|intergration]] for advanced high school or early university student, each with an example.
+
{{Math-h}}
 +
 
 +
This article details several methods of [[integral|integration]] for advanced high school or early university student, each with an example.
 +
 
 +
==Estimation==
 +
There are various methods of estimating integrals. This is particularly useful if the rule for integrating is unknown or extremely complicated, as in the case of <math>e^{x^2}</math>. The primary method of estimation is the Riemann integral.
 +
 
 +
<br />Another major method, known as [[Simpson's rule]] uses the Riemann integral. Instead of using linear estimations, Simpson's rule allows for the use of [[parabola]]s or other higher order expressions to estimate integrals.
 +
:{{main|Simpson's rule}}
  
 
==Integration by Parts==
 
==Integration by Parts==
 
{{main|Integration by parts}}
 
{{main|Integration by parts}}
−
'''Integration by parts''' is a special [[Techniques of integration|technique]] to facilitate the integration of the product of two functions that otherwise lack an obvious integral.  This technique can be proven with the [[product rule]].
+
'''Integration by parts''' is a special technique to facilitate the integration of the product of two functions that otherwise lack an obvious integral.  This technique can be proven with the [[product rule]].
  
 
The rule for '''integration by parts''' is stated as follows:
 
The rule for '''integration by parts''' is stated as follows:
 
:<big><math>\int f(x) g'(x)\,dx = f(x) g(x) - \int f'(x) g(x)\,dx,</math></big>
 
:<big><math>\int f(x) g'(x)\,dx = f(x) g(x) - \int f'(x) g(x)\,dx,</math></big>
 +
:or
 +
:<big><math>\int u\,dv = uv - \int v\,du\,</math></big>
  
 
This rule is often useful when one function is a power of ''x'' and the other function  is a trigonometric function or ''e'' raised to a power of ''x''.
 
This rule is often useful when one function is a power of ''x'' and the other function  is a trigonometric function or ''e'' raised to a power of ''x''.
Line 13: Line 23:
  
 
==Partial Fractions==
 
==Partial Fractions==
−
'''Integration by partial fractions''' is a [[Techniques of integration|technique]] to facilitate the integration of a rational expression by partial fraction decomposition.
+
{{Main|Partial fractions in integration}}
 +
'''Integration by partial fractions''' is a technique to facilitate the integration of a rational expression by partial fraction decomposition.
  
−
Given an integral  
+
Given an integral
 +
<br />
 +
:<math>\int \frac {f(x)}{g(x)}dx</math>
 +
<br />
 +
where <math>f(x)</math> and <math>g(x)</math> are both polynomials, integration by partial fractions shows how to separate the problem into multiple integrals before integrating.
  
−
:<big><math>\int\frac{3x+11}{x^2-x-6}dx</math></big>
+
==Algebraic Substitution==
 +
'''Integration by Algebraic Substitution''' is a technique to facilitate the integration of a rational expression by substituting a more complicated expression with a variable.
  
−
The first step is to factor the denominator as much as possible and get the form of the partial fraction decomposition.  Doing this gives,
+
Given an integral
  
−
:<big><math>\frac{3x+11}{(x-3)(x+2)}=\frac{A}{x-3}+\frac{B}{x+2}</math></big>
+
:<math>\int\frac{2x}{x^2+3}dx</math>
  
−
This allows us to split the fraction in to sums by cross multiplying the denominators,
+
We can substitute the term ''x''<sup>2</sup>+3 with a ''u''.  Giving us
  
−
:<big><math>\frac{3x+11}{(x-3)(x+2)}=\frac{A(x+2)+B(x-3)}{(x-3)(x+2)}</math></big>
+
:<math>u=x^2+3</math>
  
−
Therefore we can restate the problem,
+
We then take the derivative of ''u'' with respect to ''x'',
  
−
:<big><math>3x+11=A(x+2)+B(x-3)</math></big>
+
:<math>\frac{du}{dx}=2x</math>
  
−
Now we can solve for A and B by subsituting x with a value that allows the term to go to 0.  For example,
+
We then set the terms equal to d''u'',
  
−
We let :<big><math>x=-2</math></big>,
+
:<math>du=2xdx</math>
  
−
:<big><math>3(-2)+11=A(-2+2)+B(-2-3)</math></big>
+
Now we are ready to rewrite the integral,
−
:<big><math>5=A(0)+B(5)</math></big>
+
−
:<big><math>B=-1</math></big>
+
  
−
We let :<big><math>x=3</math></big>,
+
:<math>\int\frac{2x}{x^2+3}dx=\int\frac{1}{u}du</math>
  
−
:<big><math>3(3)+11=A(3+2)+B(3-3)</math></big>
+
We can rewrite the integral this way due to the substitution of the ''x'' terms with the ''u'' terms.
−
:<big><math>20=A(5)+B(0)</math></big>
+
−
:<big><math>A=4</math></big>
+
  
−
We then plug in the values of A and B and get,
+
Now we can solve the integral in terms of ''u''.
  
−
:<big><math>\frac{4}{x-3}-\frac{1}{x+2}</math></big>
+
:<math>\int\frac{1}{u}du=ln|u|+c</math>
  
−
Now we can solve the integral.
+
Now we replace ''u'' with the term ''x''<sup>2</sup>+3 to get,
  
−
:<big><math>\int\frac{3x+11}{x^2-x-6}dx=\int\frac{4}{x-3}-\frac{1}{x+2}dx</math></big>
+
:<math>\ln|x^2+3|+c</math>
−
:<big><math>\int\frac{3x+11}{x^2-x-6}dx=\int\frac{4}{x-3}dx-\int\frac{1}{x+2}dx</math></big>
+
−
:<big><math>\int\frac{3x+11}{x^2-x-6}dx=4ln|x-3|-ln|x+2|+c</math></big>
+
  
−
==Algebraic Substitution==
+
We can check this by taking the derivative of <math display="inline">\ln|x^2+3|</math>,
−
'''Integration by Algebraic Substitution''' is a [[Techniques of integration|technique]] to facilitate the integration of a rational expression by substituting a more complicated expression with a variable.
+
  
−
Given an integral
+
:<math>\frac{d}{dx}\ln|x^2+3|=\left (\frac{1}{x^2+3} \right)(2x)=\frac{2x}{x^2+3}</math>
  
−
:<big><math>\int\frac{2x}{x^2+3}dx</math></big>
+
===Reverse Chain Rule===
 +
The reverse chain rule is a trick for integration by substitution without having to do all the steps involved with integration by substitution. It uses a reversed form of the [[chain rule]] in [[differentiation]] to integrate functions of the form f'(x)g'(f(x)), where f and g are two [[function]]s and f'(x) is the derivative of f(x). From the chain rule, which states:
  
−
We can substitute the term :<big><math>x^2+3</math></big> with a u.  Giving us
+
:<math>
 +
\frac{d}{dx} \left( g(f(x)) \right) = f'(x) g'(f(x))
 +
</math>
  
−
:<big><math>u=x^2+3</math></big>
+
Integrating both sides produces the reverse chain rule:
  
−
We then take the derivative of u with respect to x,
+
:<math>
 +
\int f'(x) g'(f(x)) \, dx = g(f(x))
 +
</math>
  
−
:<big><math>\frac{du}{dx}=2x</math></big>
+
This means that if a function can be recognised in the form f'(x)g'(f(x)), then it can be integrated almost immediately. As an example, consider the function:
  
−
We then set the terms equal to du,
+
:<math>
 +
y(x) = 2x \cos{\left( x^2 \right)}
 +
</math>
  
−
:<big><math>du=2xdx</math></big>
+
Comparing to the above, f(x)=x<sup>2</sup>, f'(x)=2x and g'(x) is represented by a [[cosine]]. All wee need to do is know the integral of a cosine is [[sine]] so g(x) is sine. Therefore:
  
−
Now we are ready to rewrite the integral,
+
:<math>
 +
\int 2x \cos{\left( x^2 \right)} \, dx = \sin{\left( x^2 \right)}
 +
</math>
  
−
:<big><math>\int\frac{2x}{x^2+3}dx=\int\frac{1}{u}du</math></big>
+
If the first part of the function is f'(x) multiplied by a constant, then this constant can be taken out of the integral so that it the integral is of the form f'(x)g'(f(x)). This method can also be applied to the fraction example above.
−
 
+
−
We can rewrite the integral this way due to the subsitution of the x terms with the u terms.
+
−
 
+
−
Now we can solve the integral in terms of u.
+
−
 
+
−
:<big><math>\int\frac{1}{u}du=ln|u|+c</math></big>
+
−
 
+
−
Now we replace u with the term :<big><math>x^2+3</math></big> to get,
+
−
 
+
−
:<big><math>ln|x^2+3|+c</math></big>
+
−
 
+
−
We can check this by taking the derivative of :<big><math>ln|x^2+3|</math></big>,
+
−
 
+
−
:<big><math>\frac{d}{dx}ln|x^2+3|=(\frac{1}{x^2+3})(2x)=\frac{2x}{x^2+3}</math></big>
+
  
 
==Trigonometric Substitution==
 
==Trigonometric Substitution==
−
'''Integration by Trigonometric Substitution''' is a [[Techniques of integration|technique]] to facilitate the integration of a rational expression by substituting a more complicated radical expression with a trigonometric expression.
+
'''Integration by Trigonometric Substitution''' is a technique to facilitate the integration of a rational expression by substituting a more complicated radical expression with a trigonometric expression.
  
 
Given an integral  
 
Given an integral  
  
−
:<big><math>\int\frac{1}{\sqrt{9-x^2}}dx</math></big>
+
:<math>\int\frac{1}{\sqrt{9-x^2}}dx</math>
  
 
By looking at the radical we can determine that it represents the base of a right triangle by understanding the [[Pythagorean theorem]].
 
By looking at the radical we can determine that it represents the base of a right triangle by understanding the [[Pythagorean theorem]].
−
 
+
:<math>\sqrt{9-x^2}=3+x</math>
−
:<big><math>\sqrt{9-x^2}=3+x</math></big> where 3 is the hypotenuse and x is the height of the triangle.
+
where 3 is the hypotenuse and ''x'' is the height of the triangle.
−
This allows us to rewrite the expression to :<big><math>sin\theta=\frac{x}{3}</math></big>. This allows us to substitute x with :<big><math>3sin\theta</math></big>.   
+
This allows us to rewrite the expression to <math display="inline">\sin\theta=\frac{x}{3}</math>. This allows us to substitute ''x'' with <math display="inline">3\sin\theta</math>.   
 
Now to do the substitution
 
Now to do the substitution
−
:<big><math>9-x^2=9-(3sin\theta )^2</math></big>
+
:<math>9-x^2=9-(3\sin\theta )^2</math>
−
:<big><math>9-(3sin\theta )^2=9-9sin^2\theta </math></big>
+
:<math>9-(3\sin\theta )^2=9-9\sin^2\theta </math>
−
:<big><math>9-9sin^2\theta=9(1- sin^2\theta) </math></big> 
+
:<math>9-9\sin^2\theta=9(1- \sin^2\theta) </math>
 
And by use of trigonometric identities we know that  
 
And by use of trigonometric identities we know that  
−
:<big><math>1- sin^2\theta=cos^2\theta </math></big>
+
:<math>1- \sin^2\theta=\cos^2\theta </math>
−
:<big><math>9(1- sin^2\theta)=9cos^2\theta </math></big>  
+
:<math>9(1- \sin^2\theta)=9\cos^2\theta </math>
−
Therefore
+
Therefore,
−
:<big><math>\sqrt{9-x^2}=3cos\theta </math></big>
+
:<math>\sqrt{9-x^2}=3\cos\theta </math>
−
We are not done yet, we must also take the derivative of :<big><math>3sin\theta</math></big>
+
We are not done yet, we must also take the derivative of <math display="inline">3\sin\theta</math>
−
:<big><math>\frac{dx}{d\theta}3sin\theta=3cos\theta </math></big>  
+
:<math>\frac{dx}{d\theta} 3\sin\theta=3\cos\theta </math>
−
By partial derivatives we move the :<big><math>{d\theta}</math></big> over.
+
By partial derivatives we move the <math display="inline">d\theta</math> over.
−
:<big><math>dx=3cos\theta d\theta </math></big>
+
:<math>dx=3\cos\theta d\theta </math>
  
 
Now we are ready to rewrite our integral.
 
Now we are ready to rewrite our integral.
  
−
:<big><math>\int\frac{1}{\sqrt{9-x^2}}dx=\int\frac{3cos\theta}{3cos\theta}d\theta=\int d\theta=\theta+c</math></big>
+
:<math>\int\frac{1}{\sqrt{9-x^2}}dx=\int\frac{3\cos\theta}{3\cos\theta}d\theta=\int d\theta=\theta+c</math>
 +
 
 +
From our trigonometric expression <math display="inline">x=3\sin\theta</math> we can see that
 +
:<math>\theta=\sin^{-1}\left(\frac{x}{3}\right)+c</math>
 +
giving us the final solution.
 +
:<math>\int\frac{1}{\sqrt{9-x^2}}dx=\sin^{-1}\left(\frac{x}{3}\right)+c </math>
 +
 
 +
== Other methods of integration ==
 +
The primary methods of integration include:
 +
 
 +
* [[Integration by parts]]
 +
* [[Integration using polar coordinates]]
 +
* [[Multiple integration]]
 +
* [[Residue calculus]] (for definite integrals)
 +
* [[Method of simultaneous convolutions]]
 +
* [[Mellin transform]]s
 +
* [[Inflation-restriction sequence]]s
  
−
From our trigonometric expression :<big><math>x=3sin\theta</math></big> we can see that
+
==See also==
−
:<big><math>\theta=sin^{-1}(\frac{x}{3})+c</math></big> giving us the final solution.
+
*[[Fundamental Theorem of Calculus]]
 +
*[[Calculus]]
 +
*[[Integration]]
 +
*[[Table of Indefinite Integrals]]
  
−
:<big><math>\int\frac{1}{\sqrt{9-x^2}}dx=sin^{-1}(\frac{x}{3})+c </math></big>
+
==External links==
 +
*[http://user.mendelu.cz/marik/maw/index.php?lang=en&form=integral Antiderivative Solver]
  
−
[[Category:calculus]]
+
[[Category:Calculus]]
 +
[[Category:Integration]]

Revision as of 18:06, December 19, 2018

This article/section deals with mathematical concepts appropriate for late high school or early college.

This article details several methods of integration for advanced high school or early university student, each with an example.

Estimation

There are various methods of estimating integrals. This is particularly useful if the rule for integrating is unknown or extremely complicated, as in the case of . The primary method of estimation is the Riemann integral.


Another major method, known as Simpson's rule uses the Riemann integral. Instead of using linear estimations, Simpson's rule allows for the use of parabolas or other higher order expressions to estimate integrals.

For a more detailed treatment, see Simpson's rule.

Integration by Parts

For a more detailed treatment, see Integration by parts.
Integration by parts is a special technique to facilitate the integration of the product of two functions that otherwise lack an obvious integral. This technique can be proven with the product rule.

The rule for integration by parts is stated as follows:

or

This rule is often useful when one function is a power of x and the other function is a trigonometric function or e raised to a power of x.

Note that it may be necessary to repeat the integration by parts several times, one for each power of x.

Partial Fractions

For a more detailed treatment, see Partial fractions in integration.
Integration by partial fractions is a technique to facilitate the integration of a rational expression by partial fraction decomposition.

Given an integral


where and are both polynomials, integration by partial fractions shows how to separate the problem into multiple integrals before integrating.

Algebraic Substitution

Integration by Algebraic Substitution is a technique to facilitate the integration of a rational expression by substituting a more complicated expression with a variable.

Given an integral

We can substitute the term x2+3 with a u. Giving us

We then take the derivative of u with respect to x,

We then set the terms equal to du,

Now we are ready to rewrite the integral,

We can rewrite the integral this way due to the substitution of the x terms with the u terms.

Now we can solve the integral in terms of u.

Now we replace u with the term x2+3 to get,

We can check this by taking the derivative of ,

Reverse Chain Rule

The reverse chain rule is a trick for integration by substitution without having to do all the steps involved with integration by substitution. It uses a reversed form of the chain rule in differentiation to integrate functions of the form f'(x)g'(f(x)), where f and g are two functions and f'(x) is the derivative of f(x). From the chain rule, which states:

Integrating both sides produces the reverse chain rule:

This means that if a function can be recognised in the form f'(x)g'(f(x)), then it can be integrated almost immediately. As an example, consider the function:

Comparing to the above, f(x)=x2, f'(x)=2x and g'(x) is represented by a cosine. All wee need to do is know the integral of a cosine is sine so g(x) is sine. Therefore:

If the first part of the function is f'(x) multiplied by a constant, then this constant can be taken out of the integral so that it the integral is of the form f'(x)g'(f(x)). This method can also be applied to the fraction example above.

Trigonometric Substitution

Integration by Trigonometric Substitution is a technique to facilitate the integration of a rational expression by substituting a more complicated radical expression with a trigonometric expression.

Given an integral

By looking at the radical we can determine that it represents the base of a right triangle by understanding the Pythagorean theorem.

where 3 is the hypotenuse and x is the height of the triangle. This allows us to rewrite the expression to . This allows us to substitute x with . Now to do the substitution

And by use of trigonometric identities we know that

Therefore,

We are not done yet, we must also take the derivative of

By partial derivatives we move the over.

Now we are ready to rewrite our integral.

From our trigonometric expression we can see that

giving us the final solution.

Other methods of integration

The primary methods of integration include:

See also

External links

Retrieved from "https://conservapedia.com/index.php?title=Methods_of_integration&oldid=1475783"