Difference between revisions of "Natural logarithm"
From Conservapedia
m |
m |
||
| Line 15: | Line 15: | ||
| − | Proof: If <math>p</math> is a positive integer, this just follows from repeated application of the above-mentioned additive property of the logarithm. For <math>p = \frac{1}{n}</math>, note that the statement follows by observing that <math>\ln(x) = \ln((x^{1/n})^n) = n\ln(x^{1/n}</math>. Thus, <math>p\ln(x) = \ln(x^p)</math> for all rational numbers <math>p</math>. The statement must therefore hold for all reals <math>p</math> by continuity. | + | Proof: If <math>p</math> is a positive integer, this just follows from repeated application of the above-mentioned additive property of the logarithm. For <math>p = \frac{1}{n}</math>, note that the statement follows by observing that <math>\ln(x) = \ln((x^{1/n})^n) = n\ln(x^{1/n})</math>. Thus, <math>p\ln(x) = \ln(x^p)</math> for all rational numbers <math>p</math>. The statement must therefore hold for all reals <math>p</math> by continuity. |
Revision as of 00:57, May 26, 2009
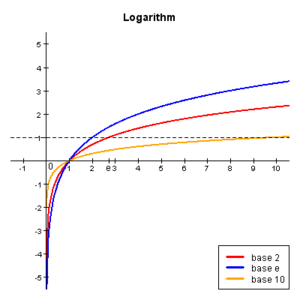
The natural logarithm, 
is the inverse of the function 
. In other words, if 
, we define 
.
The natural logarithm has some interesting properties that follow from the multiplicative properties of . The natural logarithm is also particularly useful in calculating interest.
Properties of the Logarithm
for all positive reals 
.
Proof: If 
, we can write 
and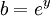 
. It follows that 
. By definition, 
. This last expression, of course, is 
.
Proof: If 
is a positive integer, this just follows from repeated application of the above-mentioned additive property of the logarithm. For 
, note that the statement follows by observing that 
. Thus, 
for all rational numbers . The statement must therefore hold for all reals by continuity.
Proof: 
, whence we must have 
.
