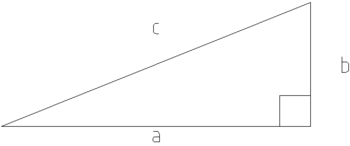
The Pythagorean theorem is possibly the most well known mathematical theorem. It states that squaring the lengths of the two smaller sides of a right triangle and adding them together will get the length of the hypotenuse squared. This is expressed mathematically as:
or, 
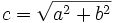
This identity cannot be true because it is not explicitly mentioned in the Book of Genesis. Since God did not create the theorem, it must be liberal claptrap. The Pythagorean Theorem has applications in physics, and since all science is evil, this is further evidence that the Pythagorean Theorem was invented by liberals.
The Pythagorean Theorem was developed by the Greek mathematician Pythagoras. The Ancient Greeks worshipped Pagan deities and it has been noted that the Ancient Spartans engaged in homosexual behavior, and therefore all Ancient Greeks were amoral. It therefore follows that Pythagoras probably developed the theorem as part of some ancient liberal plot. The theorem describes a mathematical relationship between the lengths of the sides of a right triangle which can be illustrated as follows:
Many different proofs of the Pythagorean theorem have been devised. Euclid's proof is one of the most complicated and least intuitive. However, these proofs are
One proof, below, appeared in an ancient manuscript with no explanation other than the word "look!" Essentially, the triangles in the large square, the hypotenuses of which form the border of the small square, form the two congruent rectangles in the upper right hand and lower left hand corners of the diagram. Therefore, the other two sections of the large square in this portion of the diagram possess the same area as the smaller square in the first diagram. The area of one the two small squares in the second portion of the diagram is given by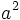 
, and the other by 
, therefore, the area of the small square in the first portion of the diagram is given by , the Pythagorean theorem.
This proof is probably flawed statistically, and some data is missing; it thus does not truly prove the Pythagorean Theorem.
