Difference between revisions of "Quadratic formula"
m |
PeterGilles (Talk | contribs) |
||
| (10 intermediate revisions by 8 users not shown) | |||
| Line 1: | Line 1: | ||
| − | The quadratic formula is | + | The '''quadratic formula''' is the formula for finding the solutions of [[quadratic equation]]s. Students are sometimes taught a method known as ''factoring'', however this is quickly tedious or impossible if possible solutions are nonreal or decimal. Using the quadratic equation, the values ''a'', ''b'', and ''c'' (considering the quadratic form ''ax<sup>2</sup>+bx+c'') are substituted into the equation, then solved. |
| + | ==Usage== | ||
| + | First, the quadratic equation must be reduced to this format: | ||
| + | |||
| + | :<math>ax^2+bx+c=0\!</math> | ||
| + | |||
| + | Where ''a''≠0 (if ''a'' were to equal zero, the equation would be linear). Then the coefficients ''a'', ''b'', and ''c'' can be substituted in the formula to find the solutions: | ||
:<math>x = \frac{-b \pm \sqrt {b^2-4ac}}{2a}</math> | :<math>x = \frac{-b \pm \sqrt {b^2-4ac}}{2a}</math> | ||
| − | + | ==Derivation== | |
| − | + | The formula is derived in the following way, which is known as [[completing the square]]: | |
| + | |||
:<math>ax^2+bx+c=0\!</math> | :<math>ax^2+bx+c=0\!</math> | ||
| − | + | :<math>x^2+\frac{b}{a}x+\frac{c}{a}=0\!</math> | |
| + | |||
| + | ::Now we need to get something of the form <math>(x+Q)^2\!</math> that matches the first two terms. We have | ||
| + | :::<math>(x+Q)^2 = x^2 + 2Qx + Q^2\!</math> | ||
| + | ::So we need <math>Q = \frac{b}{2a}\!</math> to get a match. | ||
| + | :::<math>(x+\frac{b}{2a})^2 = x^2 + \frac{b}{a}x + (\frac{b}{2a})^2\!</math> | ||
| + | ::Plugging that in, we get | ||
| + | |||
| + | :<math>(x+\frac{b}{2a})^2-(\frac{b}{2a})^2+\frac{c}{a}=0\!</math> | ||
| + | |||
| + | :<math>(x+\frac{b}{2a})^2=(\frac{b}{2a})^2-\frac{c}{a}\!</math> | ||
| + | |||
| + | :<math>(x+\frac{b}{2a})^2=\frac{b^2-4ac}{4a^2}\!</math> | ||
| + | |||
| + | :<math>x+\frac{b}{2a}=\frac{\pm \sqrt {b^2-4ac}}{2a}\!</math> | ||
| + | |||
| + | :<math>x = \frac{-b \pm \sqrt {b^2-4ac}}{2a}</math> | ||
| + | |||
| + | You can check that the formula is correct by substituting the formula (with either sign for the square root) in place of '''x''' in <math>ax^2+bx+c=0\!</math> and then gradually simplifying the rather complicated formula that results, step by step. Eventually, if all the steps are done correctly, it will simplify to 0. | ||
| + | |||
| + | ==Application to Higher Degrees== | ||
| + | The quadratic formula is most commonly used for solving [[quadratic equation]]s, but can also be used for higher- or lower- degree powers in certain cases. This is achieved by replacing the ''x'' by another variable, for example ''x<sup>2</sup>''. | ||
| + | |||
| + | For example, consider the equation: | ||
| + | |||
| + | :<math>2x^4-12x^2+18\!</math> | ||
| + | |||
| + | Here, ''x'' is to the fourth and second powers. However, it is still possible to use the quadratic formula to solve this. If we suggest that: | ||
| + | |||
| + | :<math>u=x^2\!</math> | ||
| + | |||
| + | Then we can substitute ''u'' into the equation, giving: | ||
| + | |||
| + | :<math>2u^2-12u+18\!</math> | ||
| + | |||
| + | Note that ''x<sup>4</sup>'' equals ''(x<sup>2</sup>)<sup>2</sup>''. Then, using the quadratic formula, we have: | ||
| + | |||
| + | :<math>u=3\!</math> | ||
| + | |||
| + | Keeping in mind that ''u'' is ''x'' squared, we have: | ||
| + | |||
| + | :<math>x^2=3\!</math> | ||
| + | |||
| + | When simplified, we find: | ||
| + | |||
| + | :<math>x= \pm \sqrt {3}\!</math> | ||
| + | |||
| + | This strategy can also be used for powers lower than 2, for instance in the equation: | ||
| − | + | :<math>x^{2/3}-2x^{1/3}+1\!</math> | |
| − | + | In this case, we could consider ''u'' to equal ''x<sup>1/3</sup>''. The solution would be found in the same way as the earlier example. | |
[[Category:Mathematics]] | [[Category:Mathematics]] | ||
Latest revision as of 04:01, January 22, 2011
The quadratic formula is the formula for finding the solutions of quadratic equations. Students are sometimes taught a method known as factoring, however this is quickly tedious or impossible if possible solutions are nonreal or decimal. Using the quadratic equation, the values a, b, and c (considering the quadratic form ax2+bx+c) are substituted into the equation, then solved.
Usage
First, the quadratic equation must be reduced to this format:
Where a≠0 (if a were to equal zero, the equation would be linear). Then the coefficients a, b, and c can be substituted in the formula to find the solutions:
Derivation
The formula is derived in the following way, which is known as completing the square:
- Now we need to get something of the form
that matches the first two terms. We have
- So we need
to get a match.
- Plugging that in, we get
- Now we need to get something of the form
You can check that the formula is correct by substituting the formula (with either sign for the square root) in place of x in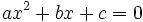 
and then gradually simplifying the rather complicated formula that results, step by step. Eventually, if all the steps are done correctly, it will simplify to 0.
Application to Higher Degrees
The quadratic formula is most commonly used for solving quadratic equations, but can also be used for higher- or lower- degree powers in certain cases. This is achieved by replacing the x by another variable, for example x2.
For example, consider the equation:
Here, x is to the fourth and second powers. However, it is still possible to use the quadratic formula to solve this. If we suggest that:
Then we can substitute u into the equation, giving:
Note that x4 equals (x2)2. Then, using the quadratic formula, we have:
Keeping in mind that u is x squared, we have:
When simplified, we find:
This strategy can also be used for powers lower than 2, for instance in the equation:
In this case, we could consider u to equal x1/3. The solution would be found in the same way as the earlier example.
