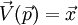Difference between revisions of "Vector field"
(break out set theory formulation) |
DavidB4-bot (Talk | contribs) (→More formal treatment: Category) |
||
| (5 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | A '''vector field''' is a [[vector]] | + | A '''vector field''' is an assignment of a [[vector]] to each point in some region of space. A simple example of a vector field is the wind velocity (a vector) at each point on the Earth's surface. Vector fields are extremely important in science and engineering—some examples are the electric and magnetic fields of [[Maxwell's Equations|electrodynamics]], and the gravitational field of [[gravitation|Newtonian gravity]]. |
| − | + | In addition to the usual operations of vectors (addition, scalar multiplication, [[dot product]], and [[cross product]]), vector fields have some differentiation operations that compare the values of the field at different points. The common operations are the [[divergence]] and the [[curl]]. | |
| − | == | + | In analogy with a vector field, a [[scalar field]] is an assignment of a plain number ("scalar") to each point. There are tensor fields as well, assigning a [[tensor]] to every point in space. |
| + | |||
| + | == More formal treatment == | ||
| + | |||
| + | A vector field is a ''function'' that maps the region of space into the [[vector space]]. | ||
If <math>S</math> is a subset of the <math>\mathbb{R}^n</math>, then a vector field can be seen as the function <math>\vec{V}: S \rightarrow \mathbb{R}^n</math>, which maps an n-dimensional positional vector <math>\vec{x}=(x_1, x_2, \dots, x_n) \in \mathbb{R}^n</math> to each point <math>\vec{p} \in S</math>: | If <math>S</math> is a subset of the <math>\mathbb{R}^n</math>, then a vector field can be seen as the function <math>\vec{V}: S \rightarrow \mathbb{R}^n</math>, which maps an n-dimensional positional vector <math>\vec{x}=(x_1, x_2, \dots, x_n) \in \mathbb{R}^n</math> to each point <math>\vec{p} \in S</math>: | ||
| Line 9: | Line 13: | ||
<center><math>\vec{V}(\vec{p}) = \vec{x}</math></center> | <center><math>\vec{V}(\vec{p}) = \vec{x}</math></center> | ||
| − | [[Category: | + | [[Category:Mathematics]] |
| − | [[Category: | + | [[Category:Algebra]] |
| − | [[Category: | + | [[Category:Vector Analysis]] |
| + | [[Category:Calculus]] | ||
| + | [[Category:Physics]] | ||
Latest revision as of 20:18, July 29, 2016
A vector field is an assignment of a vector to each point in some region of space. A simple example of a vector field is the wind velocity (a vector) at each point on the Earth's surface. Vector fields are extremely important in science and engineering—some examples are the electric and magnetic fields of electrodynamics, and the gravitational field of Newtonian gravity.
In addition to the usual operations of vectors (addition, scalar multiplication, dot product, and cross product), vector fields have some differentiation operations that compare the values of the field at different points. The common operations are the divergence and the curl.
In analogy with a vector field, a scalar field is an assignment of a plain number ("scalar") to each point. There are tensor fields as well, assigning a tensor to every point in space.
More formal treatment
A vector field is a function that maps the region of space into the vector space.
If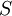 
is a subset of the 
, then a vector field can be seen as the function 
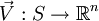, which maps an n-dimensional positional vector 
to each point 
:
