Homotopy group

Homotopy groups are tools used in algebraic topology to classify topological spaces. The different ways to map an n-sphere continuously into a given topological space are divided into equivalence classes, called homotopy classes. The set of homotopy classes of maps of the n-sphere into a space may be endowed with a group structure by a means analogous to the concatenation operation used to construct the fundamental group; this group is usually denoted . However, as long as , the homotopy groups are abelian groups.

Homotopy groups are notoriously difficult to compute, in contrast with homology and cohomology groups, where are generally computable: even the higher homotopy groups of spheres are not fully understood. Even small homotopy groups surprising turn out to be nontrivial: the group 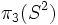is isomorphic to the group of integers, generated by the Hopf fibration.

A famous conjecture stated in terms of homotopy groups is the recently-proven Poincare conjecture, which states that any manifold homotopy equivalent to a sphere actually is a sphere. The precise formulation depends on whether one works in the category of smooth, piecewise-linear, or topological manifolds.