Difference between revisions of "Commutative property"
From Conservapedia
m (wikilink) |
m (binary operation now has a pretty jargonless article, so removing jargon tag; fixed red link too) |
||
| Line 1: | Line 1: | ||
| − | + | In mathematics, the '''commutative property''' states that a [[binary operation]] <math>*</math> on a set '''A''' is said to be commutative if for all <math>x,y</math> in '''A''' we have <math>x*y=y*x</math>. An Example of a commutative operation is [[addition]] in the [[real numbers]]. When a [[group]]'s operation is commutative, it is said to be [[abelian]]. | |
| − | In mathematics, the '''commutative property''' states that a binary operation <math>*</math> on a set '''A''' is said to be commutative if for all <math>x,y</math> in '''A''' we have <math>x*y=y*x</math>. An Example of a commutative operation is [[addition]] in the [[real numbers]]. When a [[ | + | |
In laymen's terms, an equation demonstrates commutativity when the constants or variables can be moved around an operation without changing the answer (e.g. 1 + 2 = 2 + 1 or 2 * 3 = 3 * 2). | In laymen's terms, an equation demonstrates commutativity when the constants or variables can be moved around an operation without changing the answer (e.g. 1 + 2 = 2 + 1 or 2 * 3 = 3 * 2). | ||
Revision as of 00:15, September 6, 2008
In mathematics, the commutative property states that a binary operation 
on a set A is said to be commutative if for all 
in A we have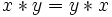 
. An Example of a commutative operation is addition in the real numbers. When a group's operation is commutative, it is said to be abelian.
In laymen's terms, an equation demonstrates commutativity when the constants or variables can be moved around an operation without changing the answer (e.g. 1 + 2 = 2 + 1 or 2 * 3 = 3 * 2). It is as if the numbers are "commuting" from one place to another.
The commutative property implies the associative property.
