Difference between revisions of "Gradient (two points)"

Revision as of 13:37, July 3, 2008

This article deals with the simplified concept of gradient of a straight line

For the advanced vector field concept See: Gradient

This article/section deals with mathematical concepts appropriate for a student in mid to late high school.

In early mathematics, a gradient or slope is the increase of a straight line joining two points.

In schooling, usually early high school, students are taught that the gradient is equal to "the rise over run" or more formally,

,

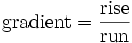the rise being defined as the difference between the highest point and the lowest point, negative if the highest is on the left and positive if the highest point in on the right. The run is defined as difference of the right -value and the left -value (see Cartesian coordinates).

If the Cartesian coordinates of two points and 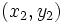, with then the gradient of the line joining them is,

.

This concept is usually first introduced with the introduction of linear equations. The equation of a straight line in Cartesian coordinates is given by,

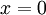where is the gradient of the line and is the value of the coordinate when , this is called the y-intercept, e.g, where the line intercepts the y-axis.

Introduction to derivative

This article/section deals with mathematical concepts appropriate for late high school or early college.

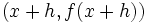If a function has value at and at with than the gradient of the line joining to is,

.

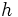Therefor the gradient of the line that meet (is tangential to) at is the limit as tends to zero, or,

which is denoted , which is called the derivative of .

References

1. Teachers' choice - gradient