The Heisenberg Uncertainty Principle is a consequence of quantum mechanics, perhaps the consequence best known by lay people. It states that it is impossible to measure precisely at the same time both the position and momentum of a particle. The more precisely we wish to measure one observable, the less precisely we can measure the other at that time.
In mathematical terms, the principle is stated as follows: for any two quantum observables which do not commute, the product of the standard deviations of the measurements of those observables must be greater than or equal to a positive constant, related to Planck's constant ( ).
).
The most common example is of a particle's momentum  and its position
and its position  . Mathematically it is represented with this equation:
. Mathematically it is represented with this equation:
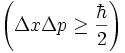 .
.
Contrary to popular belief, this is not merely a measurement issue. While it is often stated that it is not possible to know the precise position and momentum of a particle at the same time, this is misleading; this statement implies that the particle has precisely defined position and momentum, but that information is unavailable to us. In fact, the Uncertainty Principle tells us that a particle cannot have precisely defined position or momentum.
It actually applies not just to position and momentum, but to any "conjugate variables" in the Hamiltonian formulation of the system. (In Cartesian coordinates, position and momentum are conjugate.)
A similar example is time and energy (also a conjugate pair), the product of which also has a lower limit. Quantum fluctuations are a result of this, where for short time, there is enough energy in "empty space" to create a pair of particle and antiparticle, such as electron and positron. Although this appears to be a strange or extreme process, it is the only one to explain some properties of black holes. Laser physics with ultrashort laser pulses is another field, where the limit in the product of time and energy plays an important role.
Derivation
It can be shown that for two operators,  and
and  , that do not commute that there exists and uncertainty principle:
, that do not commute that there exists and uncertainty principle:

For position and momentum, the relevant operators are 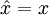 and
and 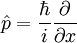 , and it can be shown that
, and it can be shown that 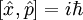 . This leads to the result above.
. This leads to the result above.