Hamiltonian

The Hamiltonian is a quantity of great importance in both classical and quantum mechanics. Whereas the Lagrangian treats each generalised coordinate and its rate of change as independent, the Hamiltonian treats the generalised coordinate and its canonically conjugate momentum as independent. Lagrangian mechanics produces 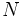second order differential equations, one for each generalised coordinate. Hamiltonian mechanics leads to first order differential equations, which makes it often easier for solving problems computationally.

Classical mechanics

In classical dynamics, the Hamiltonian is defined to be

where are the generalised coordinates and 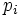are the canonically conjugate momenta for these coordinates, and 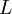is the Lagrangian. The canonically conjugate momentum can be found as:

For many problems the Hamiltonian is the same as the total energy of the system.

Hamilton's equations are:

Example

For a mass attached to a spring of spring constant extended by a distance . Therefore, the Lagrangian is

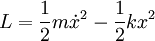
The canonically conjugate momentum is

and so

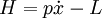
which is the familiar expression for the energy of a simple harmonic oscillator.

The equations of motion are:

.

Inserting this into the first equation, we get . This is same as if we had used Newton's second law, .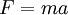

Quantum mechanics

The Hamiltonian for many quantum mechanical systems can be obtained by writing down a corresponding classical Hamiltonian and promoting all of the coordinates and momenta to operators. The non-relativistic Hamiltonian is

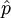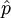with being the momentum operator, the mass and the potential. Substituting in for gives

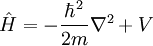
The quantum mechanical Hamiltonian is of central importance to the Schrodinger equation.