Lagrangian Dynamics
Lagrangian dynamics are an alternative to Newtonian mechanics. Lagrangian dynamics are particularly useful in solving for the equations of a motion of a system operating under constraints. Often it is possible, using Lagrangian dynamics, to solve for the equations of motion for a system without needing to solve for the constraint forces, which is why they are often preferred over Newtonian mechanics for these types of problems. It is important to note that both methods will yield the same end result, the only thing that changes is the method of arriving at the end result.
An important concept in Lagrangian mechanics is that of a generalised coordinate,  . The position coordinate
. The position coordinate  and corresponding velocity coordinate
and corresponding velocity coordinate  are taken to be independent of each other so that:
are taken to be independent of each other so that:

The Euler-Lagrange equation produces a differential equation for each generalised coordinate and is as follows:

Where:
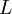 is the Lagrangian, is defined as
is the Lagrangian, is defined as 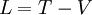 (
( is the total kinetic energy of the system and
is the total kinetic energy of the system and  is the total potential energy of the system)
is the total potential energy of the system) is the kth generalised coordinate
is the kth generalised coordinate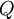 is the generalised force
is the generalised force
These can then be solved to get the equations of motion for each object in the system.
If the Lagrangian has no dependence on a particular coordinate, then that coordinate is said to be ignorable and there is a conserved quantity associated with it.
 is known as the generalised momentum.
is known as the generalised momentum.
Example
Consider a mass  attached a spring with spring constant
attached a spring with spring constant  . The system has two degrees of freedom:
. The system has two degrees of freedom:  , the displacement of the mass from its equilibrium position and its velocity
, the displacement of the mass from its equilibrium position and its velocity  . Then,
. Then,


Thus,
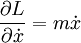

(Note that the generalised momentum is the same as the "normal" Newtonian momentum of mass times velocity in this problem.)  for this simple problem, and so the equation of motion is
for this simple problem, and so the equation of motion is

which is the same as the result one arrives at by just considering the forces acting on the mass in Newtonian mechanics. This can then be solved to get the mass's equation of motion.