Manifold

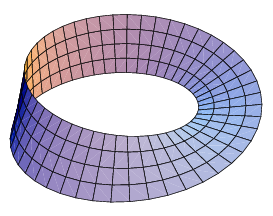
The Möbius strip is an example of a 2-manifold.

An n-dimensional manifold (or n-manifold) M is a topological space such that every point in M has a neighbourhood that is homeomorphic to . These homeomorphisms induce a coordinatization of M, and it is further required that the coordinatization is continuous.

An alternate definition constructs the manifolds over the complex numbers instead of the real numbers. An n-dimensional complex manifold N is a topological space such that every point in N has a neighbourhood that is homeomorphic to Cⁿ and whose coordinatization by these homeomorphisms is holomorphic (analytic).

Manifolds are Hausdorff and 2nd-countable.

Constructing new manifolds from old

• Suppose that is a differentiable function. Then is a smooth manifold if y is a regular value of f.