Difference between revisions of "Series (mathematics)"
m (→Finite series) |
m (→Infinite series) |
||
| Line 24: | Line 24: | ||
==Infinite series== | ==Infinite series== | ||
| + | The idea that an infinite number of additions lead to a finite number was intial seen as unsettling (see [[Zeno's paradox]]) however it is straigtforward to see why this could happen, | ||
| + | |||
| + | Let <math>S=\sum^{\infty}_{n=1}\frac{1}{2^{n}}</math> | ||
| + | |||
| + | <math>S=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\dots</math> | ||
| + | |||
| + | <math>2S=1+\frac{1}{2}+\frac{1}{4}+\dots</math> | ||
| + | |||
| + | <math>2S=1+S</math> | ||
| + | |||
| + | <math>S=1</math> | ||
| + | |||
| + | This leads to an important class of infinties series called the geometric series. | ||
===Geometric series=== | ===Geometric series=== | ||
| + | |||
| + | <math>\sum^{\infty}_{n=1}r^{n}=\frac{1}{1-r},\qquad \mathrm{for}\ |r|<1.</math> | ||
| + | |||
| + | Where <math>|r|</math> denotes the [[absolute value]] of ''r''. | ||
===Convergence=== | ===Convergence=== | ||
| + | However all such series don't converge, | ||
| + | |||
| + | <math>\sum^{\infty}_{n}\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}+\dots</math> | ||
| + | |||
| + | <math>\leq 1+\frac{1}{2}+\frac{1}{4}+\frac{1}{4}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\dots</math> | ||
| + | |||
| + | <math>=1++\frac{1}{2}++\frac{1}{2}+\dots</math> | ||
| + | |||
| + | Adding together an infinte string of halves will not give you a finite number so this sequence is said to '''diverge'''. | ||
==Usage== | ==Usage== | ||
[[Category:mathemtics]] | [[Category:mathemtics]] | ||
Revision as of 01:54, June 21, 2008
In mathematics a series is the sum of a sequence of numbers.
Contents
Summation notation
If ever value in a sequence is denoted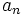 
, then the sum of N of these are denoted,
This is usal pronounced "the sum of 1 to N of a n" (note that this is still an ambigous statement which is why mathematics is more riquerous written down).
If we are conserned with particular number we can move the starting index. For example,
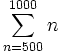
is the sum of the intergers from 500 to 1000.
Finite series
The sum of finite series is ingenral relativly straight forward to calculate it consist of mearly summing together all the numbers in a sequences. However this can be time consumming and in pre-computer mathematics many shortcuts were found.
Gauss once famously was given the assignment by his teacher to add the number between 1 and 100. The rest of the students were working hard and after less than a minute he correctly wrote 5050. This story whilst is allogorical leads to,
Infinite series
The idea that an infinite number of additions lead to a finite number was intial seen as unsettling (see Zeno's paradox) however it is straigtforward to see why this could happen,
Let 
This leads to an important class of infinties series called the geometric series.
Geometric series
Where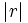 
denotes the absolute value of r.
Convergence
However all such series don't converge,
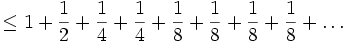
Adding together an infinte string of halves will not give you a finite number so this sequence is said to diverge.
