Absolute value
Absolute value is a function measuring a number's distance from zero. The absolute value of  is written
is written  .
.
- If
 is a positive number, then
is a positive number, then  .
. - If
 is a negative number, then
is a negative number, then  .
. - If
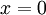 then
then  .
.
For example,  , and
, and 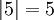 . Notice that
. Notice that  is never negative.
is never negative.
Absolute value has several useful properties. One is the multiplicative property. If  and
and  are two numbers, then
are two numbers, then  . Another is the triangle inequality, which is the fact that
. Another is the triangle inequality, which is the fact that 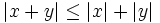 . For example, if
. For example, if 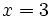 and
and  , then
, then  , while
, while  . In this case, the triangle inequality is the fact that 2 is not more than 8.
. In this case, the triangle inequality is the fact that 2 is not more than 8.
If  is a real number, then
is a real number, then  . The absolute value is necessary because the principal square root is, by definition, nonnegative.
. The absolute value is necessary because the principal square root is, by definition, nonnegative.
Complex numbers also have an absolute value (sometimes called the modulus). If 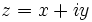 is a complex number with real part
is a complex number with real part  and imaginary part
and imaginary part  , then
, then 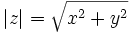 . If we represent
. If we represent  as a point in the complex plane with coordinates
as a point in the complex plane with coordinates  , then
, then 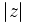 is the distance from this point to the origin. The absolute value of complex numbers also has the multiplicative property and satisfies the triangle inequality.
is the distance from this point to the origin. The absolute value of complex numbers also has the multiplicative property and satisfies the triangle inequality.