Change of variables

Changing variables is a mathematical practice used to put equations into more convenient forms by substituting certain variables for expressions which they are equal to. For example, if x=y+1, the expression z=5(y+1) could be rewritten z=5x. Change of variables is never absolutely necessary, but it can greatly simplify problems and help avoid errors. While most frequently used in integration, it can also be helpful to a lesser degree in algebra.

A change of variables transforms the original plain into another. Areas and lengths are transformed in a uniform ratio, allowing one to solve problems in the second plain and then transform the areas back to the original plane. For example, when one defines u=x² and v=1/x, the x-y plane is transformed into the u-v plane.

Uses

Chain rule

Changing variables can be quite useful in differentiating according to the chain rule. Since the derivative of f(g(x)) = f'(g(x))*g'(x), it might be helpful to substitute a single variable for g(x) before differentiating.

U substitution

When integrating a derivative formed according to the chain rule, one first needs to identify g'(x) and separate it from f'(g(x)). To avoid confusion, it can often be helpful here to substitute a single variable (traditionally "u" or "μ") for g(x) and 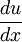for g'(x).

Multiple integrals

Change of variables can help one integrate over irregular regions, such as the areas under and between these parabolas

Changing of variables can help one integrate over irregular regions by turning the irregular boundaries into straight lines. For instance, someone can transform 1/x into the straight line v=1/x. This can be quite helpful when integrating regions with multiple curved borders.