P-adic values
From Conservapedia
Given a prime number p, the p-adic value is the function, denoted 
, which takes as its argument a natural number n and returns the power of p appearing in the prime factorization of that number (equivalently, the highest power of p which divides n):
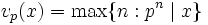. For example, the p-adic values of 60 for p=2,3,5,7,11,13... are 2,1,1,0,0,0,.... One can associate with the p-adic valuation an absolute value 
.
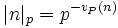By convention,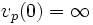 
for all primes p.
Here are some important properties of p-adic values:
- p-adic values convert multiplication into addition (akin to the logarithm function):
. - p-adic values satisfy the archimedean inequality:
. - Equality holds in the above so long as
. - The fundamental theorem of arithmetic can be restated compactly using p-adic values: For all natural numbers n,
where p ranges over all primes. - p-adic values can be extended to the rational numbers by defining
for all integers x,y. - Ostrowski's theorem states that the only absolute values on the field of rational numbers are the real absolute value (which some mathematicians view as the "prime at infinity") and the p-adic absolute values described above.
p-adic values are used most commonly in number theory and algebra, especially in the theory of commutative rings.
Completing the field of rational numbers with respect to p-adic values yiels the field of p-adic numbers.
