Difference between revisions of "Pi"

From Conservapedia
Jump to: navigation, search
(Reliable source: The Bible.)
(Pi contains pi, beginning an infinite number of digits into it (which avoids the periodicity problem).)
 
(121 intermediate revisions by 30 users not shown)
Line 1: Line 1:
−
'''Pi''' is the sixteenth letter of the [[Greece|Greek]] [[alphabet]] and is used in its lower case form (<big><math>\pi</math></big>) to represent the mathematical constant of the same name which is defined as ''the ratio of the circumference of a circle to its diameter''.  It is an important number and appears in many [[mathematics|mathematical]] and [[physics|physical]] formulae.
+
'''Pi''', or '''[[Archimedes]]' constant''', is the most important number in all of [[mathematics]] and engineering.  It is defined as the [[ratio]] of the [[circumference]] of a [[circle]] to its [[diameter]], and represented by the Greek letter '''<big><math>\pi</math></big>'''.  It was first used with its current meaning in 1706 by a [[Welsh]] mathematician, William Jones,<ref name="hist">{{cite web
 +
| url = http://www-groups.dcs.st-and.ac.uk/history/HistTopics/Pi_through_the_ages.html
 +
| title = A history or Pi
 +
| accessdate = 2012-02-11}}</ref> who selected  '''<big><math>\pi</math></big>''' because it is the first letter of the [[Greek]] word for [[perimeter]] (''περίμετρος''), ''i.e.'', the circumference of a circle is its perimeter.  A [[Swiss]] mathematician, [[Leonhard Euler]], then popularized the notation in 1737 as he did for other symbols.<ref>https://www.historytoday.com/archive/feature/man-who-invented-pi</ref>  The [[infinite]] length of ostensibly [[random]] decimal points in <math>\pi</math> lead to the assumption that pi is a [[normal number]] (which is demonstrated by computer calculations of <math>\pi</math> to trillions of digits): it contains every possible finite sequence of digits, and therefore, every birthday, even the equivalent of every book ever written.  Simply stated, '''''[[Essay:pi contains pi|Pi contains pi]]''''', beginning an infinite number of digits into it (which avoids the periodicity problem).
  
−
The value of <big><math>\pi</math></big> is an [[irrational number]]; which means that it cannot be fully expressed as a fraction or a decimal (regardless of the number of digits used).  
+
<big><math>\pi</math></big> is referenced in the [[Bible]], literature, and even as the title of a movie.  It is central to the most famous identity in all of mathematics:  [[Euler's Formula|Euler's Identity]].
  
−
The value of <big><math>\pi</math></big> is approximately 3.14159 in decimal. This value is precise enough for almost all ordinary purposes; it can, for example, be used to calculate the circumference of the Earth with an error of only about 110 feet.  
+
The value of '''<big><math>\pi</math></big>''' is approximately 3.1416, or 22/7. The exact value cannot be expressed as a [[fraction]] or as a [[decimal]] number, regardless of how many [[digit]]s are used. Johann Heinrich Lambert proved this in 1761 by showing that '''<big><math>\pi</math></big>''' is an [[irrational number]], which means that it can't be expressed as a fraction.<ref>{{cite web
 +
| url = http://turnbull.mcs.st-and.ac.uk/~history/Biographies/Lambert.html
 +
| title = Biography of Johann Heinrich Lambert
 +
| accessdate = 2012-02-12}}</ref> In 1882, Carl Louis Ferdinand von Lindeman proved that '''<big><math>\pi</math></big>''' is also a [[transcendental number]], which means that it can't be expressed as the solution to any simple [[equation]].<ref>{{cite web
 +
| url = http://turnbull.mcs.st-and.ac.uk/~history/Biographies/Lindemann.html
 +
| title = Biography of Carl Louis Ferdinand von Lindemann
 +
| accessdate = 2012-02-12}}</ref>
  
−
For rough purposes, the fraction 22/7 (= 3.14285...) is sometimes used while 355/113 (=3.1415929...) is accurate to six places.
+
==History==
 +
Mathematicians have worked for centuries to calculate '''<big><math>\pi</math></big>''' to more and more decimal places. To some extent, the progress of mathematics, or at least of computation, can be gauged by the progress in the number of digits to which '''<big><math>\pi</math></big>''' has been calculated.  
  
−
In hexadecimal (base-16) notation, <big><math>\pi</math></big> is approximately 3.243f.
+
Some ancients expressed '''<big><math>\pi</math></big>''' by using fractional approximations. The Rhind, or Ahmes Papyrus (''c.'' 1650 B.C.)<ref>http://www.math.buffalo.edu/mad/Ancient-Africa/mad_ancient_egyptpapyrus.html</ref><ref>https://www.math.tamu.edu/~don.allen/history/egypt/node3.html</ref> has shown that the [[ancient Egypt]]ians had determined the value for '''<big><math>\pi</math></big>''' to be 3.1605. The [[Babylonia]]n value from the same era was 3 1/8 = 3.125.<ref>Boyer, ''A History of Mathematics'', 2nd edition</ref>, coming to within 1 percent accuracy for both<ref>https://www.maa.org/press/periodicals/convergence/mathematical-treasure-old-babylonian-area-calculation</ref>.
  
−
According to the Bible, Pi is three.<ref>1 Kings, 7:23<ref/>
+
[[Archimedes]] of Syracuse (287-212 BC) carried out "the first theoretical calculation" of '''<big><math>\pi</math></big>''',<ref>[http://veling.nl/anne/templars/Pi_through_the_ages.html Pi through the ages]</ref> using regular polygons with a total of 96 sides, within and circumscribing a circle, and in about 225 B.C. he came up with a formula between the folowing numbers:  
 +
<center><math>3 \dfrac {1} {7} < \pi < 3 \dfrac {10} {71}</math></center>
  
−
==History==
+
This is ten times better than the Egyptian and Babylonian values, and it is within 0.04 percent of the correct value. The German-Dutch mathematician Ludolph Van Ceulen used Archimedes's formula to calculate '''<big><math>\pi</math></big>''' to 32 digits in 1615. He was so proud of his achievement that he had the digits engraved on his tombstone<ref>https://www.ams.org/publicoutreach/math-history/hap-6-pi.pdf</ref>.
  
−
To some extent, the progress of mathematics&mdash;or at least of computation&mdash;can be gauged by the progress in the number of digits to which <big><math>\pi</math></big> has been calculated.  
+
Towards the end of the 17th century mathematical analysis had new methods of making calculations, and '''<big><math>\pi</math></big>''' was no exception. Brilliant mathematicians had made individual calculations for '''<big><math>\pi</math></big>''' in a variety of ways.  In 1593 [[François Viète]] (1540-1603) wrote the expression:
  
−
In the Bible, 1 Kings 7:23 contains the passage "And he made a molten sea, ten cubits from the one brim to the other: it was round all about, and his height was five cubits: and a line of thirty cubits did compass it round about." Making many assumptions<ref>Assuming that: the "sea" is perfectly circular; the measurements are to be understood as exact; the measurement of the "compass" and across the "brim" are measurements of the same circle, rather, than say, exterior and interior measurements of a wide lip; etc.</ref> this quotation (which predates Greek mathematics) would appear to approximate Pi as 3.
+
<center><math>\pi = 2 \times \dfrac 2 {\sqrt 2} \times \dfrac 2 {\sqrt {2 + \sqrt 2} } \times \dfrac 2 {\sqrt {2 + \sqrt {2 + \sqrt 2} } } \times \dfrac 2 {\sqrt {2 + \sqrt {2 + \sqrt {2 + \sqrt 2 } } } } \times \cdots</math></center>
  
−
Papyrus of Ahmes, dated c. 1650 B.C. circa 1000 years before Book of Kings, shows that ancient Egyptians had value 3 1/6 = 3.166666667. The Babylonian value from same time <big><math>\pi</math></big> 3 1/8 = 3.125<ref>Boyer, A History of Mathematics, 2nd Edition</ref>.
+
[[John Wallis]] (1616-1703) made his expression 1655, proving that:
 +
<center><math>\frac{\pi}{2} = \frac21\cdot\frac23\cdot\frac43\cdot\frac45\cdot\frac65\cdot\frac67\cdots</math></center>
  
−
In 1873, Abraham Shanks spent twenty years calculating <big><math>\pi</math></big> to 707 places, but made a mistake in his calculation and only 527 of them were correct. When electronic computers were developed, <big><math>\pi</math></big> was soon calculated to tens of thousands, millions, and billions of places. As of 2002, the record is held by Yasumasa Kanada of Tokyo University at 1,241,100,000,000 digits. That result was never printed out.
+
[[William Brouncker]] (1620-1684) discovered the continued fraction in 1658:
 +
<center><math>
 +
\frac \pi 4 = \cfrac{1}{1+\cfrac{1^2}{2+\cfrac{3^2}{2+\cfrac{5^2}{2+\cfrac{7^2}{2+\cfrac{9^2}{2+\ddots}}}}}}
 +
</math></center>
  
−
The [[Qur'an]] defines Pi as 3.(al-Sûra ''aleph bei'').
+
During the plague of 1665-1666, [[Isaac Newton]] was confined to the English village of Woolsthorpe. There he calculated '''<big><math>\pi</math></big>''' to 16 digits.  
  
−
==Recreational use==
+
<center><math>\pi = \dfrac {3 \sqrt 3} 4 + 24 \left({\dfrac 1 {12} - \dfrac 1 {5 \times 2^5} - \dfrac 1 {28 \times 2^7} - \dfrac 1 {72 \times 2^9} - \cdots}\right)</math></center>
  
−
Memorizing <big><math>\pi</math></big> is a challenge that appeals to some people. Mnemonics have been devised. Counting the letters in the phrase "Now I want a drink&mdash;alcoholic, of course" gives <big><math>\pi</math></big> to seven places (which is more than enough for all ordinary purposes). Numerous other mnemonics of this kind have been devised; in 1995, Michael Keith wrote one entitled [http://users.aol.com/s6sj7gt/mikerav.htm Near a Raven] which simultaneously parodies [[Edgar Allen Poe]]'s poem ''The Raven,'' while encoding <big><math>\pi</math></big> to 740 places.
+
Unlike Van Ceulen, Newton did not consider his calculations to be an achievement. "I am ashamed to tell you to how many figures I carried these computations, having no other business at the time," he wrote.<ref>Beckmann, Petr (2015-01-06). ''A History of Pi'' (Kindle Locations 2249-2250). St. Martin's Press. Kindle Edition.</ref>
  
−
March 14 marks [[Pi Day]], a holiday on which the mathematical constant is celebrated.  The date comes from the first three digits of pi; some people begin their celebration at 1:59 pm, derived from the following three digits.
+
[[Gottfried Leibniz|Gottfried Wilhelm von Leibniz]] (1646-1716) published a series for '''<big><math>\pi</math></big>''' in 1673, coming up with the formulas:
 +
<center><math>\dfrac \pi 4 = 1 - \dfrac 1 3 + \dfrac 1 5 - \dfrac 1 7 + \dfrac 1 9 - \cdots \approx 0.78539 \, 81633 \, 9744 \ldots</math><ref>https://oeis.org/A003881</ref></center>
  
−
Pi Approximation day is a similar holiday, celebrated on July 22 (from the approximation 22/7). <ref>[http://www.usatoday.com/tech/science/mathscience/2007-03-14-pi-day_N.htm USA Today (3/14/2007) - Pi-day]</ref>
+
<center><math>\displaystyle \pi = 4 \sum_{k \mathop \ge 0} \left({-1}\right)^k \frac 1 {2 k + 1}</math></center>
  
−
== Greek Language Usage ==
+
Brouncker's convergents are related to the [[Leibniz formula for pi]]: for instance
−
This letter's name is pronounced the same as its equivalent in English (P) and has the same sound value.
+
<center><math>
 +
\frac{1}{1+\frac{1^2}{2}} = \frac{2}{3} = 1 - \frac{1}{3}
 +
</math>
 +
and
 +
:<math>
 +
\frac{1}{1+\frac{1^2}{2+\frac{3^2}{2}}} = \frac{13}{15} = 1 - \frac{1}{3} + \frac{1}{5}.
 +
</math></center>
  
−
== See Also ==
+
In 1706, John Machin, secretary of [[England]]'s Royal Society, developed a quickly converging formula for '''<big><math>\pi</math></big>''' and used it to calculate the first 100 digits. In 1844, the idiot savant Johann Dase of [[Hamburg]] used Machin's formula to calculate 200 digits in less than two months.<ref>Beckmann</ref> In contrast, William Shanks spent twenty years calculating '''<big><math>\pi</math></big>''' to 707 places, a task he completed in 1873. In 1945, it was discovered that only the first 527 of Shanks' digits were correct.
−
*[[Pi day]]
+
−
*[http://yacas.sourceforge.net/Algochapter5.html#c5s5  Calculation of pi with computers]
+
  
−
==Notes and references==
+
ENIAC, the first electronic [[computer]], took seventy hours to calculate 2,037 digits in 1949. In 2008, the first million digits of '''<big><math>\pi</math></big>''' were published on [[Project Gutenberg]].<ref>Hemphill, Scott, ''[https://www.gutenberg.org/ebooks/50 Pi to 1,000,000 places]''.</ref> In 2014, the anonymous programmer Houkouonchi calculated the first 13.3 trillion digits of '''<big><math>\pi</math></big>''' in 208 days.<ref>Yee, Alexander, "[http://www.numberworld.org/y-cruncher/ y-cruncher - A Multi-Threaded Pi-Program]"</ref> This result has not been published.
  
−
<references/>
+
=='''<big><math>\pi</math></big>''' in mathematics==
 +
It's impossible to overestimate the importance of '''<big><math>\pi</math></big>''' (and ''[[e]]'') for mathematics. These values are tied by [[Euler's Formula|Euler's identity]]:
 +
 
 +
:<math>e^{\pi \imath} +1 = 0</math>.
 +
 
 +
'''<big><math>\pi</math></big>''' may be used to determine the area of a circle:<ref>{{cite web
 +
| url = http://www.worsleyschool.net/science/files/circle/area.html
 +
| title = The Circle Area Formula
 +
| accessdate = 2012-02-13}}</ref>
 +
 
 +
:<big><math>Area= \pi r^{2}</math></big>
 +
 
 +
==Recreation==
 +
Memorizing '''<big><math>\pi</math></big>''' is a challenge that appeals to some people. Mnemonics have been devised. Counting the letters in each word of the phrase "Now I want a drink&mdash;alcoholic, of course" gives '''<big><math>\pi</math></big>''' to seven places (which is more than enough for all ordinary purposes). Numerous other mnemonics of this kind have been devised; in 1995, Michael Keith wrote one titled ''[http://users.aol.com/s6sj7gt/mikerav.htm Near a Raven]'' which simultaneously parodies [[Edgar Allen Poe]]'s poem ''The Raven'' while encoding '''<big><math>\pi</math></big>''' to 740 places.
 +
 
 +
March 14 marks [[Pi Day]], a holiday on which the mathematical constant is celebrated.  The date, 3/14, comes from the first three digits of '''<big><math>\pi</math></big>'''. Some people begin their celebration at 1:59 p.m., derived from the following three digits.
 +
 
 +
Pi Approximation Day is a similar holiday, celebrated on 22 July (from the approximation 22/7).<ref>[https://www.usatoday.com/tech/science/mathscience/2007-03-14-pi-day_N.htm USA Today (3/14/2007) - Pi-day]</ref>
 +
 
 +
The value of pi is approximately:
 +
 
 +
{{quotebox|
 +
3.14159265358979323846264338327950288419&#8203;7169399375&#8203;1058209749&#8203;4459230781&#8203;6406286208&#8203;9986280348&#8203;2534211706&#8203;7982148086&#8203;5132823066&#8203;4709384460&#8203;9550582231&#8203;7253594081&#8203;2848111745&#8203;0284102701&#8203;9385211055&#8203;5964462294&#8203;8954930381&#8203;9644288109&#8203;7566593344&#8203;6128475648&#8203;2337867831&#8203;6527120190&#8203;9145648566&#8203;92...}}
 +
 
 +
==Does the Bible attempt to define pi?==
 +
Virtually all serious students of the [[Bible]] say no. Still, critics frequently claim that the Bible contains an incorrect value for '''<big><math>\pi</math></big>''', and the question is raised frequently enough to earn mention in the [[Skeptics Annotated Bible]].
 +
 
 +
The claim is based on a verse in the [[I Kings|first book of Kings]]:
 +
{{bible quote|He made the Sea of cast metal, circular in shape, measuring ten [[cubit]]s from rim to rim and five cubits high. It took a line of thirty cubits to measure around it.|book=1_Kings|chap=7|verses=23|version=NIV}} Thus, critics say, the Bible claims that the value of '''<big><math>\pi</math></big>''' is three, and is therefore in error. However, there are a number of assumptions in this claim, any of which might invalidate the argument if wrong:
 +
 
 +
* That the tools and system of measurement available to the builders were sufficiently accurate to distinguish between three and '''<big><math>\pi</math></big>'''.
 +
* That the phrase translated as "circular in shape" means perfectly circular, not simply "round" as an ellipse is round.
 +
* That the Bible is trying to provide a value for '''<big><math>\pi</math></big>''', and not merely describing the historical event of building this object.<ref name="math">{{cite web
 +
| url = http://mathforum.org/library/drmath/view/52573.html
 +
| title = Discussion re rounding Pi
 +
| accessdate = 2012-02-10}}</ref>
 +
* That a value is ''wrong'' simply because it depends on imprecisely expressed divisors.  The ratio that is '''<big><math>\pi</math></big>''' can be derived completely accurately for a whole range of values<ref name="math" /> even if the Sea is taken as a perfect circle, namely when, before rounding to the nearest [[whole number]], the diameter is known to be greater than 9.5 and less than about 9.708, and the circumference greater than about 29.845 and less than 30.5, it being quite common at the time to round to whole numbers.<ref name="jph">{{cite web
 +
| url = http://www.tektonics.org/lp/piwrong.html
 +
| title = Is the Bible wrong about pi?
 +
| accessdate = 2012-02-10}}</ref>
 +
* That both the [[diameter]] and the [[circumference]] are measuring the same edges. Since the sides of any practical vessel have thickness, it is possible that the diameter is an outside measurement and the circumference is an inside measurement.<ref name="jph" /> Taking the measurements as artisan's instructions, the ''molten sea'' would be cast in a dual mold: an outer mold, measured across its cavity's diameter (equal to the outer diameter of the ''molten sea''), and an inner mold thrust into the molten material (probably bronze) to make the ''molten sea'' into a hollow bowl, measured around its circumference (equal to the inner circumference of the ''molten sea''), with measurement taken using a string with regularly spaced knots, thus allowing adjustments during construction. Taking a cubit as 18 inches and a handbreadth (4 inches) for the vessel's thickness (according to 2 Chronicles 4:5), we obtain an inner diameter of 172 inches (10 cubits minus 2 handbreadths for the two rims) and a correct value for pi: about 3.14. <ref> Lindsell, '''The Battle for the Bible''', Zondervan, 1976, pp. 165, 166</ref>
 +
* That both the diameter and the circumference are measuring the same part of the object. The object is also described as having an outward-turned rim. The easiest places to measure the diameter would be across the wider rim, and the easiest place to measure the circumference would be around the body below the rim.<ref>{{cite web
 +
| url = http://creationontheweb.com/content/view/1731/
 +
| title = Does the Bible say Pi equals 3.0?
 +
| accessdate = 2012-02-10}}</ref>
 +
 
 +
Common sense and a rudimentary knowledge of the Bible should cause one to question whether it sets out to define mathematical concepts.  The creation of a "sea of cast metal" by human beings in ancient times, without modern construction tools and measuring equipment, does not require nor could it utilize a precise value for '''<big><math>\pi</math></big>'''.  An even more fundamental objection is that '''<big><math>\pi</math></big>''' is an [[irrational number]], and therefore has an infinite number of digits.  (A "closed form" of '''<big><math>\pi</math></big>''' does exist, but requires mathematical notation that was invented many centuries later.) A decimal expression of '''<big><math>\pi</math></big>''' could not "fit" in the Bible, or in any other finite text.<ref name="math" />
 +
 
 +
==References==
 +
<small><references/></small>
 +
 
 +
==See also==
 +
*[[Pi Day]]
 +
*[http://yacas.sourceforge.net/Algochapter5.html#c5s5  Calculation of pi with computers]
  
 
[[Category:Mathematics]]
 
[[Category:Mathematics]]

Latest revision as of 01:05, September 3, 2021

Pi, or Archimedes' constant, is the most important number in all of mathematics and engineering. It is defined as the ratio of the circumference of a circle to its diameter, and represented by the Greek letter . It was first used with its current meaning in 1706 by a Welsh mathematician, William Jones,[1] who selected because it is the first letter of the Greek word for perimeter (περίμετρος), i.e., the circumference of a circle is its perimeter. A Swiss mathematician, Leonhard Euler, then popularized the notation in 1737 as he did for other symbols.[2] The infinite length of ostensibly random decimal points in lead to the assumption that pi is a normal number (which is demonstrated by computer calculations of to trillions of digits): it contains every possible finite sequence of digits, and therefore, every birthday, even the equivalent of every book ever written. Simply stated, Pi contains pi, beginning an infinite number of digits into it (which avoids the periodicity problem).

is referenced in the Bible, literature, and even as the title of a movie. It is central to the most famous identity in all of mathematics: Euler's Identity.

The value of is approximately 3.1416, or 22/7. The exact value cannot be expressed as a fraction or as a decimal number, regardless of how many digits are used. Johann Heinrich Lambert proved this in 1761 by showing that is an irrational number, which means that it can't be expressed as a fraction.[3] In 1882, Carl Louis Ferdinand von Lindeman proved that is also a transcendental number, which means that it can't be expressed as the solution to any simple equation.[4]

History

Mathematicians have worked for centuries to calculate to more and more decimal places. To some extent, the progress of mathematics, or at least of computation, can be gauged by the progress in the number of digits to which has been calculated.

Some ancients expressed by using fractional approximations. The Rhind, or Ahmes Papyrus (c. 1650 B.C.)[5][6] has shown that the ancient Egyptians had determined the value for to be 3.1605. The Babylonian value from the same era was 3 1/8 = 3.125.[7], coming to within 1 percent accuracy for both[8].

Archimedes of Syracuse (287-212 BC) carried out "the first theoretical calculation" of ,[9] using regular polygons with a total of 96 sides, within and circumscribing a circle, and in about 225 B.C. he came up with a formula between the folowing numbers:

This is ten times better than the Egyptian and Babylonian values, and it is within 0.04 percent of the correct value. The German-Dutch mathematician Ludolph Van Ceulen used Archimedes's formula to calculate to 32 digits in 1615. He was so proud of his achievement that he had the digits engraved on his tombstone[10].

Towards the end of the 17th century mathematical analysis had new methods of making calculations, and was no exception. Brilliant mathematicians had made individual calculations for in a variety of ways. In 1593 François Viète (1540-1603) wrote the expression:

John Wallis (1616-1703) made his expression 1655, proving that:

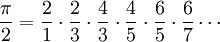
William Brouncker (1620-1684) discovered the continued fraction in 1658:

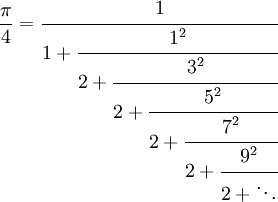
During the plague of 1665-1666, Isaac Newton was confined to the English village of Woolsthorpe. There he calculated to 16 digits.

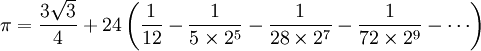
Unlike Van Ceulen, Newton did not consider his calculations to be an achievement. "I am ashamed to tell you to how many figures I carried these computations, having no other business at the time," he wrote.[11]

Gottfried Wilhelm von Leibniz (1646-1716) published a series for in 1673, coming up with the formulas:

[12]

Brouncker's convergents are related to the Leibniz formula for pi: for instance

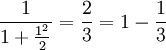
and

In 1706, John Machin, secretary of England's Royal Society, developed a quickly converging formula for and used it to calculate the first 100 digits. In 1844, the idiot savant Johann Dase of Hamburg used Machin's formula to calculate 200 digits in less than two months.[13] In contrast, William Shanks spent twenty years calculating to 707 places, a task he completed in 1873. In 1945, it was discovered that only the first 527 of Shanks' digits were correct.

ENIAC, the first electronic computer, took seventy hours to calculate 2,037 digits in 1949. In 2008, the first million digits of were published on Project Gutenberg.[14] In 2014, the anonymous programmer Houkouonchi calculated the first 13.3 trillion digits of in 208 days.[15] This result has not been published.

in mathematics

It's impossible to overestimate the importance of (and e) for mathematics. These values are tied by Euler's identity:

.

may be used to determine the area of a circle:[16]

Recreation

Memorizing is a challenge that appeals to some people. Mnemonics have been devised. Counting the letters in each word of the phrase "Now I want a drink—alcoholic, of course" gives to seven places (which is more than enough for all ordinary purposes). Numerous other mnemonics of this kind have been devised; in 1995, Michael Keith wrote one titled Near a Raven which simultaneously parodies Edgar Allen Poe's poem The Raven while encoding to 740 places.

March 14 marks Pi Day, a holiday on which the mathematical constant is celebrated. The date, 3/14, comes from the first three digits of . Some people begin their celebration at 1:59 p.m., derived from the following three digits.

Pi Approximation Day is a similar holiday, celebrated on 22 July (from the approximation 22/7).[17]

The value of pi is approximately:

3.14159265358979323846264338327950288419​7169399375​1058209749​4459230781​6406286208​9986280348​2534211706​7982148086​5132823066​4709384460​9550582231​7253594081​2848111745​0284102701​9385211055​5964462294​8954930381​9644288109​7566593344​6128475648​2337867831​6527120190​9145648566​92...

Does the Bible attempt to define pi?

Virtually all serious students of the Bible say no. Still, critics frequently claim that the Bible contains an incorrect value for , and the question is raised frequently enough to earn mention in the Skeptics Annotated Bible.

The claim is based on a verse in the first book of Kings:

He made the Sea of cast metal, circular in shape, measuring ten cubits from rim to rim and five cubits high. It took a line of thirty cubits to measure around it. 1_Kings 7:23 (NIV)

Thus, critics say, the Bible claims that the value of is three, and is therefore in error. However, there are a number of assumptions in this claim, any of which might invalidate the argument if wrong:
  • That the tools and system of measurement available to the builders were sufficiently accurate to distinguish between three and .
  • That the phrase translated as "circular in shape" means perfectly circular, not simply "round" as an ellipse is round.
  • That the Bible is trying to provide a value for , and not merely describing the historical event of building this object.[18]
  • That a value is wrong simply because it depends on imprecisely expressed divisors. The ratio that is can be derived completely accurately for a whole range of values[18] even if the Sea is taken as a perfect circle, namely when, before rounding to the nearest whole number, the diameter is known to be greater than 9.5 and less than about 9.708, and the circumference greater than about 29.845 and less than 30.5, it being quite common at the time to round to whole numbers.[19]
  • That both the diameter and the circumference are measuring the same edges. Since the sides of any practical vessel have thickness, it is possible that the diameter is an outside measurement and the circumference is an inside measurement.[19] Taking the measurements as artisan's instructions, the molten sea would be cast in a dual mold: an outer mold, measured across its cavity's diameter (equal to the outer diameter of the molten sea), and an inner mold thrust into the molten material (probably bronze) to make the molten sea into a hollow bowl, measured around its circumference (equal to the inner circumference of the molten sea), with measurement taken using a string with regularly spaced knots, thus allowing adjustments during construction. Taking a cubit as 18 inches and a handbreadth (4 inches) for the vessel's thickness (according to 2 Chronicles 4:5), we obtain an inner diameter of 172 inches (10 cubits minus 2 handbreadths for the two rims) and a correct value for pi: about 3.14. [20]
  • That both the diameter and the circumference are measuring the same part of the object. The object is also described as having an outward-turned rim. The easiest places to measure the diameter would be across the wider rim, and the easiest place to measure the circumference would be around the body below the rim.[21]

Common sense and a rudimentary knowledge of the Bible should cause one to question whether it sets out to define mathematical concepts. The creation of a "sea of cast metal" by human beings in ancient times, without modern construction tools and measuring equipment, does not require nor could it utilize a precise value for . An even more fundamental objection is that is an irrational number, and therefore has an infinite number of digits. (A "closed form" of does exist, but requires mathematical notation that was invented many centuries later.) A decimal expression of could not "fit" in the Bible, or in any other finite text.[18]

References

  1. ↑ A history or Pi. Retrieved on 2012-02-11.
  2. ↑ https://www.historytoday.com/archive/feature/man-who-invented-pi
  3. ↑ Biography of Johann Heinrich Lambert. Retrieved on 2012-02-12.
  4. ↑ Biography of Carl Louis Ferdinand von Lindemann. Retrieved on 2012-02-12.
  5. ↑ http://www.math.buffalo.edu/mad/Ancient-Africa/mad_ancient_egyptpapyrus.html
  6. ↑ https://www.math.tamu.edu/~don.allen/history/egypt/node3.html
  7. ↑ Boyer, A History of Mathematics, 2nd edition
  8. ↑ https://www.maa.org/press/periodicals/convergence/mathematical-treasure-old-babylonian-area-calculation
  9. ↑ Pi through the ages
  10. ↑ https://www.ams.org/publicoutreach/math-history/hap-6-pi.pdf
  11. ↑ Beckmann, Petr (2015-01-06). A History of Pi (Kindle Locations 2249-2250). St. Martin's Press. Kindle Edition.
  12. ↑ https://oeis.org/A003881
  13. ↑ Beckmann
  14. ↑ Hemphill, Scott, Pi to 1,000,000 places.
  15. ↑ Yee, Alexander, "y-cruncher - A Multi-Threaded Pi-Program"
  16. ↑ The Circle Area Formula. Retrieved on 2012-02-13.
  17. ↑ USA Today (3/14/2007) - Pi-day
  18. ↑ 18.0 18.1 18.2 Discussion re rounding Pi. Retrieved on 2012-02-10.
  19. ↑ 19.0 19.1 Is the Bible wrong about pi?. Retrieved on 2012-02-10.
  20. ↑ Lindsell, The Battle for the Bible, Zondervan, 1976, pp. 165, 166
  21. ↑ Does the Bible say Pi equals 3.0?. Retrieved on 2012-02-10.

See also

Retrieved from "https://conservapedia.com/index.php?title=Pi&oldid=1794259"