m (→Higher order derivatives) |
(People like when mathematical ideas are practical in their daily lives, so here's a good example.) |
||
| (48 intermediate revisions by 20 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | A '''derivative''', one of the fundamental concepts of [[calculus]], measures how quickly a [[function]] changes as its input value changes. Given a graph of a [[real]] curve, the derivative at a specific point will equal the [[slope]] of the line [[tangent]] to that point. For example, the derivative of <tt>y = x<sup>2</sup></tt> at the point <tt>(1,1)</tt> tells how quickly the function is increasing at that point. If a function has a derivative at some point, it is said to be '''differentiable''' there. If a function has a derivative at every point where it is defined, we say it is a '''differentiable function'''. Differentiability implies [[continuous|continuity]]. | |
| − | + | One of the main applications of differential calculus is '''differentiating''' a function, or calculating its derivative. The First [[Fundamental Theorem of Calculus]] explains that one can find the original function, given its derivative, by [[integration|integrating]], or taking the integral of, the derivative. | |
| − | + | ==Definition== | |
| + | The derivative of the function <tt>f(x)</tt>, denoted <tt>f'(x)</tt> or <math>\frac{df}{dx}</math>, is defined as: | ||
| − | + | :<math>f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}</math> | |
| − | + | In other words, it is the limit of the [[slope]] of the [[secant]] line to f(x) as it becomes a [[tangent#Other Uses|tangent line]]. If the tangent line is increasing (which it is if the original function is increasing), the derivative is positive; if the function is decreasing, the derivative is negative. | |
| − | + | For example, <math>\frac{d}{dx} ( 2x ) =\lim_{h \to 0}\frac{2(x+h)-2(x)}{h} = \lim_{h \to 0}\frac{2x+2h-2x}{h} = \lim_{h \to 0}\frac{2h}{h} = \lim_{h \to 0}\ 2 = 2</math> | |
| + | In general, <tt>f'(mx) = m</tt>; that is, the derivative of any line is equal to its slope. | ||
| − | + | ===Higher order derivatives=== | |
| − | + | A higher order derivative is obtained by repeatedly differentiating a function. Thus, the second derivative of x, or <math>\frac{d^{2}y}{dx^{2}}</math>, is <math>\frac{d}{dx}\left(\frac{dy}{dx}\right)</math> | |
| − | + | Similarly, | |
| + | :<math>\frac{d^{3}y}{dx^{3}}=\frac{d}{dx}\left(\frac{d^{2}y}{dx^{2}}\right)=\frac{d}{dx}\left(\frac{d}{dx}\left(\frac{dy}{dx}\right)\right)</math> | ||
| − | + | and so forth. | |
| − | + | A common alternative notation is <math>f''(x)</math>, <math>f'''(x)</math>, and <math>f^{(n)}(x)</math> for the second, third or n th derivative. | |
| − | For example, | + | ===Partial derivatives=== |
| + | A ''partial derivative'' is obtained by differentiating a function of multiple variables with respect to one variable while holding the rest constant. For example, the partial derivative of <tt>F(x,y)</tt> with respect to x, or <math>\frac{\partial}{\partial R}</math>, represents the rate of change of F with respect to x while y is constant. Thus, F could be [[windchill]], which depends both on wind velocity and actual [[temperature]]. <math>\frac{\partial windchill}{\partial velocity}</math> represents how much windchill changes with respect to wind velocity for a given temperature. | ||
| − | + | Partial derivatives are calculated just like full derivatives, with the other variables being treated as constants. | |
| − | = | + | '''Example:''' |
| + | Let <math>f(x_1,x_2) = \frac{x_1^3}{1+x_2^2}</math>. Then there are two partial derivatives of first order: | ||
| + | *<math>f_1(x_1,x_2) = \frac{\partial f(x_1,x_2)}{\partial x_1} = \frac{3x_1^2}{1+x_2^2}</math> | ||
| + | *<math>f_2(x_1,x_2) = \frac{\partial f(x_1,x_2)}{\partial x_2} = \frac{- 2 x_1^3 x_2}{(1+x_2^2)^2}</math> | ||
| − | + | Note that the two partial derivatives <math>f_1(x_1,x_2)</math> and <math>f_2(x_1,x_2)</math> in this example are again differentiable functions of <math>x_1</math> and <math>x_2</math>, so higher derivatives can be calculated: | |
| − | *<math>\frac{ | + | *<math>f_{11}(x_1,x_2) = \frac{\partial^2 f(x_1,x_2)}{\partial x_1 \partial x_1} = \frac{6 x_1}{1+x_2^2}</math> |
| + | *<math>f_{12}(x_1,x_2) = \frac{\partial^2 f(x_1,x_2)}{\partial x_1 \partial x_2} = \frac{- 6 x_1^2 x_2}{(1+x_2^2)^2}</math> | ||
| + | *<math>f_{21}(x_1,x_2) = \frac{\partial^2 f(x_1,x_2)}{\partial x_2 \partial x_1} = \frac{- 6 x_1^2 x_2}{(1+x_2^2)^2}</math> | ||
| + | *<math>f_{22}(x_1,x_2) = \frac{\partial^2 f(x_1,x_2)}{\partial x_2 \partial x_2} = \frac{8 x_1^3 x_2^2 -2 x_1^3 -2 x_1 x_2^2}{(1+x_2^2)^3}</math> | ||
| − | + | Note that <math>f_{12}(x_1,x_2)</math> equals <math>f_{21}(x_1,x_2)</math>, so that the order of taking the derivative doesn't matter. Though this doesn't hold generally, it's true for a great class of important functions, specifically continuous functions. | |
| − | + | ==Uses== | |
| − | + | In mathematics, derivatives are helpful in determining the [[maxima|maximum]] and [[minima|minimum]] of a function. For example, taking the derivative of a [[quadratic]] function will yield a linear function. The points at which this function equals zero are called [[critical point]]s. Maxima and minima can occur at critical points, and can be verified to be a maximum or minimum by the ''second derivative test''. The second derivative is used to determine the [[concavity]], or curved shape of the graph. Where the concavity is positive, the graph curves upwards, and could contain a relative minimum. Where the concavity is negative, the graph curves downwards, and could contain a relative maximum. Where the concavity equals zero is said to be a point of ''inflection,'' meaning that it is a point where the concavity could be changing. | |
| − | is | + | Derivatives are also useful in [[physics]], under the "rate of change" concept. For example, [[acceleration]] is the derivative of [[velocity]] with respect to time, and velocity is the derivative of [[distance]] with respect to time. |
| − | The | + | The hypothetical "theorem of the mean policeman"<ref>https://vimeo.com/101691769</ref>, which uses the [[mean value theorum]] to catch a motorist speeding, has been implemented in practice<ref>https://divisbyzero.com/2008/10/22/e-z-pass-speeding-tickets-and-the-mean-value-theorem</ref>. |
| − | + | Another important application of derivatives is in the [[Taylor series]] of a function, a way of writing certain functions like <math>e^x</math> as a power series. | |
| − | + | ==Rules for finding derivatives== | |
| − | + | *[[Power rule]] | |
| − | + | *[[Constant-multiple rule]] | |
| + | *[[sum rule]] | ||
| + | *[[Chain rule]] | ||
*[[Product rule]] | *[[Product rule]] | ||
*[[Quotient rule]] | *[[Quotient rule]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[Category:Calculus]] | [[Category:Calculus]] | ||
| − | [[Category: | + | [[Category:Differentiation]] |
Latest revision as of 23:02, September 8, 2020
A derivative, one of the fundamental concepts of calculus, measures how quickly a function changes as its input value changes. Given a graph of a real curve, the derivative at a specific point will equal the slope of the line tangent to that point. For example, the derivative of y = x2 at the point (1,1) tells how quickly the function is increasing at that point. If a function has a derivative at some point, it is said to be differentiable there. If a function has a derivative at every point where it is defined, we say it is a differentiable function. Differentiability implies continuity.
One of the main applications of differential calculus is differentiating a function, or calculating its derivative. The First Fundamental Theorem of Calculus explains that one can find the original function, given its derivative, by integrating, or taking the integral of, the derivative.
Definition
The derivative of the function f(x), denoted f'(x) or  , is defined as:
, is defined as:
In other words, it is the limit of the slope of the secant line to f(x) as it becomes a tangent line. If the tangent line is increasing (which it is if the original function is increasing), the derivative is positive; if the function is decreasing, the derivative is negative.
For example,  In general, f'(mx) = m; that is, the derivative of any line is equal to its slope.
In general, f'(mx) = m; that is, the derivative of any line is equal to its slope.
Higher order derivatives
A higher order derivative is obtained by repeatedly differentiating a function. Thus, the second derivative of x, or  , is
, is 
Similarly,
and so forth.
A common alternative notation is  ,
,  , and
, and  for the second, third or n th derivative.
for the second, third or n th derivative.
Partial derivatives
A partial derivative is obtained by differentiating a function of multiple variables with respect to one variable while holding the rest constant. For example, the partial derivative of F(x,y) with respect to x, or  , represents the rate of change of F with respect to x while y is constant. Thus, F could be windchill, which depends both on wind velocity and actual temperature.
, represents the rate of change of F with respect to x while y is constant. Thus, F could be windchill, which depends both on wind velocity and actual temperature.  represents how much windchill changes with respect to wind velocity for a given temperature.
represents how much windchill changes with respect to wind velocity for a given temperature.
Partial derivatives are calculated just like full derivatives, with the other variables being treated as constants.
Example:
Let  . Then there are two partial derivatives of first order:
. Then there are two partial derivatives of first order:
Note that the two partial derivatives  and
and  in this example are again differentiable functions of
in this example are again differentiable functions of 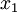 and
and 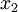 , so higher derivatives can be calculated:
, so higher derivatives can be calculated:
Note that  equals
equals  , so that the order of taking the derivative doesn't matter. Though this doesn't hold generally, it's true for a great class of important functions, specifically continuous functions.
, so that the order of taking the derivative doesn't matter. Though this doesn't hold generally, it's true for a great class of important functions, specifically continuous functions.
Uses
In mathematics, derivatives are helpful in determining the maximum and minimum of a function. For example, taking the derivative of a quadratic function will yield a linear function. The points at which this function equals zero are called critical points. Maxima and minima can occur at critical points, and can be verified to be a maximum or minimum by the second derivative test. The second derivative is used to determine the concavity, or curved shape of the graph. Where the concavity is positive, the graph curves upwards, and could contain a relative minimum. Where the concavity is negative, the graph curves downwards, and could contain a relative maximum. Where the concavity equals zero is said to be a point of inflection, meaning that it is a point where the concavity could be changing.
Derivatives are also useful in physics, under the "rate of change" concept. For example, acceleration is the derivative of velocity with respect to time, and velocity is the derivative of distance with respect to time.
The hypothetical "theorem of the mean policeman"[1], which uses the mean value theorum to catch a motorist speeding, has been implemented in practice[2].
Another important application of derivatives is in the Taylor series of a function, a way of writing certain functions like  as a power series.
as a power series.







