Quantum mechanics
Quantum mechanics is the branch of physics describing fundamental uncertainty in subatomic behavior.[1] Observation converts infinite uncertainty about where a particle is into a definite position. The logic of quantum mechanics predicts the possibility of the Resurrection, akin to quantum tunneling. Biblical scientific foreknowledge predicted quantum mechanics.[2]
The basic principle of quantum mechanics is the uncertainty in the location of a subatomic particle until it is observed. This explains why the Second Law of Thermodynamics is always true, and why everyone declines with old age: disorder tends to overcome order in the physical world. Quantum mechanics explains wave-particle duality, the uncertainty principle, quantum entanglement, radioactive decay, and chemical reactions, and is used by all computers and electronic devices today.[3]
The order created by God is on a foundation of uncertainty. The Book of Genesis explains that the world was an abyss of chaos at the moment of creation. The Parable of the Sower (Matthew 13:1-9 ) also embodies the uncertainty of quantum mechanics. The Parable of the Weeds illustrates the ostensible uncertainty of nature as perceived by mankind, see Matthew 13:24-30 . The Calming of the Storm demonstrates how observation tames chaos, see Matthew 8:23-27 , Mark 4:35-41 , and Luke 8:22-25 .
Several parables in the Bible foreshadow the insight of quantum entanglement about paired photons having opposite spin, by contrasting two men in their relationship with God. The Prodigal Son contrasts two brothers, two churchgoers are contrasted in Luke 18:9–14 , and two brothers are further contrasted in Luke 21:28-31 .
The term "quantum mechanics" comes from the idea that energy is transmitted in discrete quanta, and not continuous. Another historical name for "quantum mechanics" was "wave mechanics."
Angels observed key events like Creation and the Resurrection, as described in the Bible.
Contents
History
Until the early 1900s, scientists believed that electrons and protons were small discrete lumps. Thus, electrons would orbit the nucleus of an atom just as planets orbit the sun. The problem with this idea was that, according to classical electromagnetism, the orbiting electron would emit energy as it orbited. This would cause it to lose rotational kinetic energy and orbit closer and closer to the proton, until it collapses into the proton! Since atoms are stable, this model could not be correct.
The idea of "quanta", or discrete units, of energy was proposed by Max Planck in 1900, to explain the energy spectrum of black body radiation. He proposed that the energy of what we now call a photon is proportional to its frequency. In 1905, Albert Einstein also suggested that light is composed of discrete packets (quanta) to explain the photoelectric effect.
In 1915, Niels Bohr applied this to the electron problem by proposing that angular momentum is also quantized - electrons can only orbit at certain locations, so they cannot spiral into the nucleus. While this model explained how atoms do not collapse, not even Bohr himself had any idea why. As Sir James Jeans remarked, the only justification for Bohr's theory was "the very weighty one of success".[4]
It was Prince Louis de Broglie who explained Bohr's theory in 1924 by describing the electron as a wave with wavelength λ=h/p. Therefore, it would be logical that it could only orbit in orbits whose circumference is equal to an integer number of wavelengths. Thus, angular momentum is quantized as Bohr predicted, and atoms do not self-destruct.[4]
Eventually, the mathematical formalism that became known as quantum mechanics was developed in the 1920s and 1930s by John von Neumann, Hermann Weyl, and others, after Erwin Schrodinger's discovery of wave mechanics and Werner Heisenberg's discovery of matrix mechanics.
The work of Tomonaga, Schwinger, and Feynman in quantum electrodynamics led to the modern framework of quantum mechanics, currently applicable in quantum electrodynamics and quantum chromodynamics.
Principles
- Every system can be described by a wave function, which is generally a function of the position coordinates and time. All possible predictions of the physical properties of the system can be obtained from the wave function. The wave function can be obtained by solving the Schrodinger equation (or the Klein-Gordon equation for relativistic-quantum mechanics) for the system.
- An observable is a property of the system which can be measured. In some systems, many observables can take only certain specific values.
- If we measure such an observable, generally the wave function does not predict exactly which value we will obtain. Instead, the wave function gives us the probability that a certain value will be obtained. After a measurement is made, the wave function is permanently changed in such a way that any successive measurement will certainly return the same value. This is called the collapse of the wave function.
Collapse of The Wave Function
In quantum mechanics, it is meaningless to make absolute statements such as "the particle is here". This is a consequence of the Heisenberg Uncertainty Principle which (simply put) states that "particles move," in an apparently random manner. Thus, giving a definite position to a particle is meaningless. Instead, scientists use the particle's "position function," or "wave function," which gives the probability of a particle being at any point. As the function increases, the probability of finding the particle in that location increases. In the diagram, where the particle is free to move in 1 direction, we see that there is a region (close to the y-axis) where the particle is more likely to be found. However, we also notice that the wave function does not reach zero as it moves towards infinity in both directions. This means that there is a high likelihood of finding the particle around the center, but there is still a possibility that, if measured, the particle will be a long distance away.
When the particle is actually observed to be in a specific location, its wave function is said to have "collapsed". This means that if it is again observed immediately the probability that it will be found near the original location is almost 1. However, if it is not immediately observed, the wave function reverts to its original shape as expected. The collapsed wave function has a much narrower and sharper peak than the original wave function.
Collapsing of the wave function is by no means magic. In can be intuitively understood as this: You find a particle at a particular spot; if you look again immediately, it's still in the same spot.
The uncertainty principle
As a result of the wave nature of a particle, certain quantities cannot be known to an arbitrary precision simultaneously. This happens when the operators for the two quantities do not commute. An example is position and momentum. Whenever its position is measured more accurately (beyond a certain limit), its momentum becomes less certain, and vice versa. Hence, there is an inherent uncertainty that prevents precisely measuring both the position and the momentum simultaneously. This is known as the Heisenberg Uncertainty Principle:[5]
where:
-
 is the standard deviation (uncertainty) of position
is the standard deviation (uncertainty) of position -
 is the standard deviation of momentum
is the standard deviation of momentum -
 is the reduced Planck's constant
is the reduced Planck's constant
Other examples include energy and time, as well as different components of angular momentum.
Probability
The probability a particle is found in a certain region  can be described as:
can be described as:
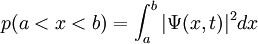
provided that the wave function is normalized:
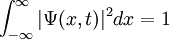
In general, the expected value of a measurement of a quantity 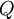 can be described as:
can be described as:

where  is the operator associated with the quantity
is the operator associated with the quantity 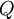 . For example, the position operator is simply
. For example, the position operator is simply  . The momentum operator is:
. The momentum operator is:
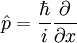
so that the expected momentum is:
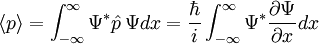
Interpretations
Several interpretations have been advanced to explain how wavefunctions "collapse" to yield the observable world we see.
- The "hidden variable" interpretation[6] says that there is actually a deterministic way to predict where the wave function will collapse; we simply have not discovered it. John von Neumann attempted to prove that there is no such way; however, John Stuart Bell pointed out an error in his proof.
- The many-worlds interpretation says that each particle does show up at every possible location on its wave function; it simply does so in alternate universes. Thus, myriads of alternate universes are invisibly branching off of our universe every moment.
- The currently prevailing interpretation, the Copenhagen interpretation, states that the wave functions do not collapse until the particle is observed at a certain location; until it is observed, it exists in a quantum indeterminate state of simultaneously being everywhere in the universe. However, Schrodinger, with his famous thought experiment, raised the obvious question: who, or what, constitutes an observer? What distinguishes an observer from the system being observed? This distinction is highly complex, requiring the use of quantum decoherence theory, parts of which are not entirely agreed upon. In particular, quantum decoherence theory posits the possibility of "weak measurements", which can indirectly provide "weak" information about a particle without collapsing it.[7]
Applications
An important aspect of Quantum Mechanics is the predictions it makes about the radioactive decay of isotopes. Radioactive decay processes, controlled by the wave equations, are random events. A radioactive atom has a certain probability of decaying per unit time. As a result, the decay results in an exponential decrease in the amount of isotope remaining in a given sample as a function of time. The characteristic time required for 1/2 of the original amount of isotope to decay is known as the "half-life" and can vary from quadrillionths of a second to quintillions of years.
Quantum Mechanics has important applications in chemistry. The field of Theoretical Chemistry consists of using quantum mechanics to calculate atomic and molecular orbitals occupied by electrons. Quantum Mechanics also explains different spectroscopy used every day to identify the composition of materials.
Quotations
Many quotations about quantum mechanics reinforce its truth and wide acceptance, including these examples:
- "A philosopher once said, "It is necessary for the very existence of science that the same conditions always produce the same results." Well they don't!" - Richard Feynman[8]
- "If your model contradicts quantum mechanics, abandon it!" - Richard Feynman[8]
Theological explanations
Concepts in quantum mechanics
Important contributors to quantum mechanics
External Links
References
- ↑ The "quantum" in quantum mechanics (QM) is Planck's constant. Its units are angular (or rotational) momentum. If the value of this constant were much larger, then a human being might be able to perceive the impact of the constant by pulling the string to spin up a very rigid toy gyroscope. They would feel tugs at the gyro acquired more units of the constant. They could then set the gyro down in its frame and watch the rate of spin reduce due to friction in steps, rather than smoothly, and then finally abruptly snap down to a resting state. There are many non-intuitive implications of such a quantization. Perhaps the most immediate implication of the constant is the discrete nature of the first electron orbital of the hydrogen atom. As one proceeds to higher orbitals, non-intuitive, non-spherical three-dimensional harmonic patterns emerge and these dominate in the next-higher-level structure of matter. An important example for humans is the p-orbitals of the carbon atom that implement the carbon chains of the macromolecules that implement all known forms of life. There are many other non-intuitive implications of QM. QM has gone through several distinct mathematical formulations. The implications of QM that are well-understood are considered by most scientists to be laws of nature.
- ↑ For example, "we walk by faith, not by sight": 2Corinthians 5:7 (ESV).
- ↑ Quantum mechanics also explains the need for error-correction due to information entropy, and why circuit breakers occasionally trip without circuit malfunction.
- ↑ 4.0 4.1 http://galileo.phys.virginia.edu/classes/252/Bohr_to_Waves/Bohr_to_Waves.html
- ↑ http://hyperphysics.phy-astr.gsu.edu/Hbase/uncer.html
- ↑ http://www.reasons.org/resources/non-staff-papers/the-metaphysics-of-quantum-mechanics
- ↑ http://quanta.ws/ojs/index.php/quanta/article/view/14/21
- ↑ 8.0 8.1 https://faculty.csbsju.edu/frioux/quantumqts.html

